席替えしたのにまた同じ席になっちゃう確率

　席替えは案外難しい。誰かに任せたら何かしら思惑が入りそうで、みんなが納得できるものになるとは限りません。かといってジャンケンしたら、アイコばかりが続いていつまで経っても決着がつかないでしょう。くじ引きするのも時間がかかります。
　さて、こういうときこそエクセルの出番です。乱数を使えば、公平でみんなが納得できる座席表を案外簡単に作れます。
　手順はこうです。まずセルA1で乱数を発生させて、セルF1まで右方向にコピーし、さらにセルF7まで下方向にコピーします。こうして42個の乱数を発生させます。次にセルA1～F7の値を大きい順に番号をつけてセルH1～M7の範囲に表示させれば完成です。そこに表示された数字を自分たちの出席番号とみなせばいいわけです。

　エクセルの関数式は、
○　セルA1の式：　　＝RAND( )
○　セルH1の式：　　＝RANK(A1 , $A$1:$F$7)

です。「数式」リボンの「シート再計算」ボタンを押せば何度でも使えますし、ファイルをコピーすれば他のクラスでも使えますからきっと重宝するはず。

　ところで、「席替えしたのにまた同じ席になっちゃったよ」という人が、クラスの中に１人以上いる確率はどれくらいになると思いますか？
　実は４人以上のクラスであれば人数に関わらず、その確率は約63％に（正確に言うと，その確率を四捨五入して小数第２位までで表すと0.63に）なります。ところで、その状況は次のケースと同じです。「クリスマス会のプレゼント交換で、みんなが持ち寄ったプレゼントを一人に１個ずつ配ったら、自分が用意したものが自分のところに来ちゃう。クリスマス会に参加したうちの誰かがそういう目にあう」、そうなる確率が約63％だということです。
　この値、意外と大きいと思うんじゃないでしょうか。しかもそれが人数に因らないということも意外なんじゃないでしょうか。

　では、計算してみましょう。「n人の人が席替えしたとき、また同じ席になっちゃう人がいる確率」を p_n とします。
○　1人で席替えしたら必ず同じ席になりますから、p₁＝1 です。
○　2人で席替えする場合、全部で2通りのうちの1通りですから、p₂＝1/2 です。
○　3人で席替えする場合、全部で3 ! = 6通りのうちの4通りですから、p₃＝4/6 です。

と、このように順番に数えていってはキリがないので、ここから先は漸化式を立てましょう。

○　「n 人の人が席替えしたとき、全員が前と異なる席になる場合の数」を a_n とします。
○　このとき「n 人の人が席替えしたとき、全員が前と異なる席になる確率」は q_n＝a_n ／n！ で、
○　「n 人の人が席替えしたとき、また同じ席になっちゃう人がいる確率」は p_n＝1－q_n です。

このとき、

○　a_n について漸化式　a_n+2＝(n＋1) (a_n+1＋a_n)　が成り立ち、…(1)
○　q_n で書き換えると、漸化式　(n＋2)q_n+2＝(n＋1)q_n+1＋q_n　となり、…(2)
○　p_n で書き換えると、漸化式　(n＋2)p_n+2＝(n＋1)p_n+1＋p_n　となって、これを解くと …(3)
○　p_n の一般項は　p_n＝1／1－1／2!＋1／3!－1／4!＋ … ＋(-1）ⁿ⁺¹／n! となります。 …(4)
※　(1) の計算法や考え方は「完全順列」というワードでネットで検索してください。
　(3) から (4) を導くのは難しいが、結果を示されれば数学的帰納法で証明できます。
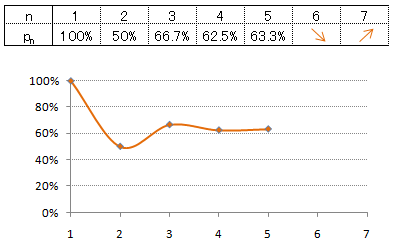
　(4) より「n が大きくなると、減衰振動します」。このことと、p₄＝0.625 , p₅＝0.633... から、４人以上の人が席替えしたとき、また同じ席になっちゃう人がいる確率は、四捨五入して 63 ％ であることが証明できます。//

ありふれた偶然　　最上位の数はどのような割合で現れるか？　　席替えしたのにまた同じ席になっちゃう確率