数学でアクティブラーニング例

　確率や場合の数（数え上げ）の問題に多いのですが、何とか値を求めたと思っても確信が持てず、他の人が求めた値と照合しても一致せず、結局正しい値がわからない、そういう数学の問題があります。
　一方で、正解を聞くと「ふむふむ、なるほど、そういうことなのね」とわかった気になります。結構簡単な問題だと思ってしまいます。
　でも、それで本当にできるようになったかというと、怪しい。似たような他の問題をやってみると、やっぱり合わない。確率や場合の数の問題は、思いのほか難しいものなのです。
　たとえば、次の問題です。

---

（東北大2014年度入試・文系後期）

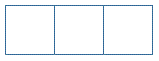
　縦横の長さの比が１：３の長方形の板がある。この板を両面とも下図のように線で区切り、できた６つの正方形のそれぞれに赤または白の色を塗ることにする。塗り終えた板において回転や裏返しで同じ塗り方になるものは区別しないとするとき、塗り方は何通りあるか求めよ。ただし、各正方形には１つの色を塗るものとする。

　この問題を次のように小分けして、高校３年生（文系）の授業でやらせました。その時間に扱うのは、この１問だけです。

(1)　６個の正方形すべて同じ色であるとき、□ 通り。
(2)　ちょうど５個の正方形が同じ色であるとき、□ 通り。
(3)　ちょうど４個の正方形が同じ色であるとき、□ 通り。
(4)　塗り方は全部で □ 通り。

---

　生徒たちが解き始めて15分くらい経ったころに、私は言いました。

隣の人の答えと比べてみな。けっこう合わないんじゃないか？

実際その通りです。みんなの答えがテンでバラバラ。自分の出した答えが合っているのかも、どれが正解なのかもわからない。そこで、次のように進めることにしました。

　自由に席を移動して、まずはお互いに答えを見せっこして、どれが正解かを探ることにしよう。答えが合わなかったら、どちらかがどこかで間違えているはずだ。それを指摘できるかな？
　２人でやれば精度は上がるけど、まだ確信は持てないね。では、どうするか。５～６人くらいでチーム作れ。そして、チーム全員が納得するまでやってみよう。
　自分の出した答えが正しいというなら、みんなに説明してみよう。説明することは自分の解き方を確認することになるし、みんなのチェックを受けることにもなる。説明を受ける側が、その答えが間違っていると思うなら、ミスを指摘してあげてくれ。
　チームで答えが一致したら、他のチームの答えと照合してごらん。答えが一致しないかもしれないよ（現にそういうケースがいくつかあった）。もし答えが一致しなかったら、チーム同士で相手のチームに説明し合ってごらん。そこでまた間違いに気づくでしょ。
　そのうちにクラス全員が同じ答えになるだろうな。そうなったら、それがきっと正解だよ。

授業残り10分になったところで、僕が出した答えを伝えました。出来ることならクラス全員の答えが一致するまでやれれば良かったんでしょうけれど、現実にはそういうわけにもいきません。

　僕が出した答えは　(1)　2通り　(2)　4通り　(3)　12通り　(4)　24通り。僕は自分で解いてみて、それから問題集に書いてある答えと照合した。だから、僕としてはたぶん合っていると思う。でも、君らの答えを見ていたら、自信が無くなってきた。
　君らが、僕の答えは間違いで、君らの答えの方が正しいと思うなら、僕に説明してくれ。僕を納得させてくれ。

結局、誰も来ませんでした。こうして（たぶん正しい）答えの数値だけを伝えて、解説などは一切なしの授業が終わりました。この日にやったのは、この１題。
　もし私が懇切丁寧に解説したら、みんなわかった気になって、でも相変わらず自力では解けないままだったことでしょう。いつの間にか、なかなか素敵なアクティブ・ラーニングの授業が出来ていました。