散らし方にも能がある

　「確率ゲーム」のサンプル問題 （→ https://omori55.blogspot.com/2019/03/blog-post_878.html ） の《解説・解答》です。

---

◇　サッカーのＰＫ戦をゲーム理論で解く
　キッカーが蹴る方向をキーパーに読まれたらゴール決定率は下がる。 キーパーが飛ぶ方向をキッカーに読まれたらゴール阻止率は下がる。 だから、キッカーは蹴る方向を、キーパーは飛ぶ方向をそれぞれ確率的に決めた方がいい。
　さて問題は、キッカーはどういう確率で蹴ればいいか、キーパーはどういう確率で飛べばいいかだ。 それぞれにとって最適な比率が各自の採るべき戦略であり、
両者がその戦略を採ったときのゴール率がゲームの解である。

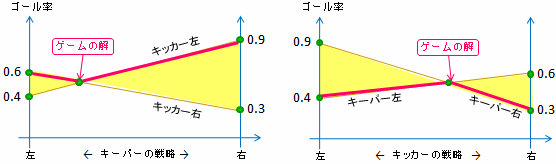
《キーパーの立場で最善策を考える》

《キッカーの立場で最善策を考える》

２本の直線はキッカーが左に蹴った場合と右に蹴った場合のゴール率（期待値）のグラフ。 　さて、キッカーがどっち蹴ろうがキーパーがどっちに飛ぼうが、ゴール率は必ず図の黄色の範囲に収まる。また、キッカーはゴール率を上げたいのだから、キッカーが合理的であればゴール率はその下限（赤線の部分）になる。 　そう考えると、上の２直線の交点がキーパーにとっての最善策ということになる。

キッカーの立場で考えても同じ。キッカーがどっちにどんな割合で蹴ろうが、キーパーがどっちにどんな割合で飛ぼうが、ゴール率は図の黄色の範囲に収まり、キーパーが合理的ならその下限（赤線部分）になる。 だから、キッカーにとっては上の２直線の交点が最も好ましいことになる。 　キッカー・キーパーにとっての最善策、ならびにそのときのゴール率を求めるには、上のグラフから相似比を使えばよい。

《拡張版利得表》

ところで、相似比は辺の長さの比であり、この場合は利得表の数の差である。また、相似比の逆比がキッカー・キーパーの採るべき戦略に、その比でゴール率の加重平均を取った値がそのときのゴール率になる。
　だから、右のように利得表の下と右に欄を付け足して数を書き込めばゲームの解が求められる。これが、確率ゲームを解くための安直法である。

　以上から、キッカーは左右に 3：5 の比で蹴り分け、キーパーは左右に 3：1 の比で飛び分けるのがそれぞれの最善策であり、双方がその戦略を採った場合のゴール率は 52.5 ％ である。

ゲーム理論・練習帳