渋滞の科学（その２）

《モデル化とシミュレーション》

（慶応大学商学部2012年度入試「論文テスト」をもとに改題）

以下の文章を読み、次の問いに答えなさい。

※ １つの【問題】を 前半 と 後半 に分けて掲載する。前半 は現実の渋滞の分析、後半 は渋滞をモデル化しシュミレーションする話。どちらか一方だけでも解答できるが、両方やれば両方の内容が符合することがわかるだろう。以下、その後半部分である。

渋滞現象をうまく表現する最も単純なモデルを紹介しよう。道路を箱の並びで表し、車を数字の１で表す。１個の箱には最大で１が１個しか入らないものとして、また車がない部分は０とする。そして「前の箱にすでに１が入って入れば動けず、０のときにのみ、前に進める」というルールをすべての１にいっせいに適用して玉を動かす。実際の動かし方だが、まずはじめの時刻で適当な０と１の並びを決めて、その状態から動ける１だけをいっせいに動かして次の時刻とする。この時間ステップを次々に繰り返していけば、１の動きは車の動きのようにも見えてくる。サーキット状の道を仮定し（図２）、サーキット内の１の数をいろいろ変えてシミュレーションして基本図を描いてみよう。密度は (6) ÷ (7) という式で表すことができるため、 (8) から (9) の値をとる。流量は、サーキット内のある１つの箱を決め、その箱を通過する１の数を調べて平均したものである。流量は平均速度がわかればそれに密度をかけて計算できる。平均速度とは、ある時刻で動いた１の数を１の総数で割った値で定義できる。平均速度は時々刻々変わるが、しばらく時間がたつと一定になる。平均速度が一定になる状態を「定常状態」といい、このときの速度を定常速度と呼ぶ。密度が (10) 以下のときは、しばらくするとすべての１が自由に動けるようになるので、定常速度は常に (11) となり、 (12) という式が成り立つ。つまり、このモデルでの臨界密度（流量が減少に転じるときの密度）は (13) で、そのときの流量は (14) となる。 密度が臨界密度より大きいときは、定常状態での流量は （１－密度） で表される。 以上のことから、_(b) この単純モデルで基本図を描くことができる 。

続いて、図２において時間経過とともに１が動く様子を、エクセルを使ってシミュレーションしてみよう。図３のようにサーキット状の道の１カ所（一番下の部分）に切り込みを入れて左右に開いて一直線状にすれば、１と０を表１のようにエクセルのセルに配置できる。このとき、１は時間経過とともに右へ移動する。まずセルA1に関数式「= Q1 を入力する。こうすることで、A列とQ列は同じ値になる。同様にセルR1に関数式「= B1 を入力する。次にセルB2に関数式

= IF (B1=0 , IF (A1=0 , (15) , (16) ) , IF (C1=0 , (17) , (18) ))

を入力して、セルQ2まで右方向にコピーすれば、スタートしてから次の時間に１がある場所が２行目に表示される。さらに、それぞれの式を下方向にコピーすれば、時間経過とともに１が動く様子をシミュレーションできる。

※ 参考文献：「クルマの渋滞、アリの渋滞」技術評論社

「渋滞学」新潮社、  いずれも西成活裕 著

問５．(6) ～ (14) に入る最も適当な数字、語句あるいは式を次の選択肢から選びなさい。
　　 なお、同じ選択肢を何回用いてもよい。
　　　　1　0　　　　　　　 2　0.5　　　　　　　　　 3　1
　　　　4　1 の総数　　　　5　0 の総数　　　　　　　6　箱の総数
　　　　7　流量＝密度　　　8　流量＝1＋密度　　　　 9　流量＝1－密度

問６．図２にはある時刻における１と０の位置が示されている。 文中の平均速度の定義に従って、図２の平均速度を小数第２位まで求めなさい。

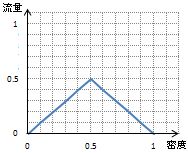
問７．(b) この単純モデルで基本図を描くことができる とあるが、単純モデルの基本図を、横軸に密度、縦軸に流量をとって描きなさい。

問８．(15) ～ (18) に 0 か 1 のいずれかを入れて、関数式を完成させなさい。

---

《 解答 》

問５．(6)　2　　　  (7)　6　　　　 (8)　1
　　　(9)　3　　　 (10)　2　　　　(11)　3
　　  (12)　7　　　(13)　2　　　　(14)　2
問６．　0.56　　　
問７．　（右グラフ）
問８．　(15)　0　　　(16)　1　　　(17)　0　　　(18)　1