角柱３本の交わり

　前の問題「角柱２本の交わり」で、角柱２本が垂直に交わるときの交わり部分について考えました。

　では、さらにもう１つ角柱を加えて、角柱３本が垂直に交わるときの交わりについて考えましょう。
　どんな形？　体積は？

---

角柱２本の交わり は右のような八面体で、底面の対角線の長さが 1 のときの体積は 1/3 でした。
　ここに３本目の角柱を突き通すと、八面体の辺の中点を通って、４ヶ所を切り落とすことになります。

　切り落とす１ヶ所の体積は、相似比を考えて、八面体の 1/16 ですから、残った部分の体積は　1/3×（1－4/16）＝ 1/4　です。
　これが、角柱３本の交わりの体積です。

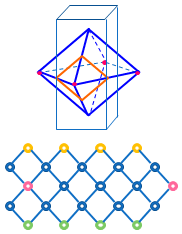
　ところでこの立体は、右のような骨組みの同じ色の点をつないでできる立体と同じです。右図の辺はどれも同じ長さですが、これを立体として組み立てると、上下の８つの四角形が縦に伸びて、中ほどの４つの四角形が横に伸びて、すべてが合同なひし形になります。
　これを「ひし形１２面体」と呼びます。正多面体ではありませんが。

角柱２本　→　円柱２本　→　角柱３本　→　円柱３本