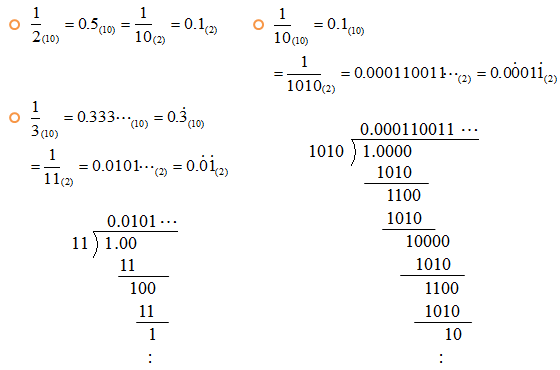見取り図３種

　　　　＜キャビネット図＞　　　　　＜等角図＞　　　　　　　＜投影図＞

◇　キャビネット図
　正面から見たときと同じ形を描き、水平線に対して 45°傾けた線上に奥行きを２分の１に縮めて描く。

◇　等角図
　幅と奥行きを水平線に対して左右に 30°傾けた線上に、幅・奥行き・高さを実際と同じ長さで描く。

◇　投影図
　正面図・平面図・側面図をそれぞれ実際と同じ形で描き、適宜かくれ線を描き、対応する部分をつなぐ。

　　　　　　　　＜方眼紙＞　　　　　　　　　　　　　　　　　＜斜眼紙＞

◇　キャビネット図と投影図は方眼紙に、等角図は斜眼紙に描くと描きやすい。
　方眼紙の斜めラインの角度 45°に沿って、キャビネット図の奥行きを伸ばせばよい。
　斜眼紙の斜めラインの角度 30°に沿って等角図の底面を、垂直方向に高さを描けばよい。

　お約束に従って、じっくり丁寧に描きながら、空間把握力を鍛えよう。次回からお題を差し上げます。

製図の基本練習

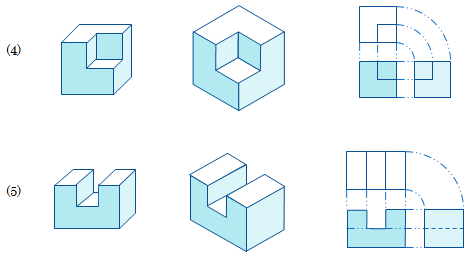
　次の立体図形のキャビネット図・等角図・投影図を、方眼紙・斜眼紙 のうちふさわしい方に描きなさい。
　なお、各問についている図は、ある面から見たときの図です。ただし、(4) では前から見ても、上から見ても、横から見てもそのように見えます。

(1)　１辺の長さが 20mm の立方体

(2)　１辺の長さが 10mm の立方体を３つ使ってできる立体

(3)　１辺の長さが 20mm の立方体を１つの平面で切ってできた立体

(4)　１辺の長さが 10mm の立方体を７つ使ってできる立体

(5)　底面が正方形である直方体の木材に溝を掘った立体

　キャビネット図・等角図・投影図の描き方のルール に従って、きれいに丁寧に描きましょう。

※ この表現で立体はそれぞれ一意に決まるはずです。
※ 方眼紙と斜眼紙（１目盛 5mm）はこちらから配りました。ピリオドをたくさん打って、自作したものです。
　当然ですが、キャビネット図と投影図は方眼紙に、等角図は斜眼紙に描くべきです。

---

　　　　　　　＜キャビネット図＞　　＜等角図＞　　　　　＜投影図＞

他は省略。

　「製図」の最初の授業で、３種類の見取り図の描き方を説明したら、さっそくこれをやります。説明の時間も合わせて２時間でなんとか仕上げてもらいます。短時間で描き上げる人もいますが、そういう人は大抵の場合ザツです。１つ１つじっくり丁寧に描きましょう。
　人によっては案外苦労するようですが、なにはともあれ３種類の見取り図を５回ずつ練習したわけです。この後、中学（技術）と 高校（情報・数学）で別系統に分かれてもう少し実践的なところに進みます。

製図のきまり

　３種類の見取り図（キャビネット図・等角図・投影図）の練習を一通りした後に、中（技術）と 高校（情報・数学）で別系統に分かれてもう少し実践的なところに進みます。以下、中学生バージョンです。

ＪＩＳ（日本工業規格）の書式は次の通りです。後ほどその書式で製図してもらいます。

まず、線は次のように描きます。

◇　外形線　　（実線・太線）
◇　かくれ線　（破線・太線）
◇　中心線　　（１点鎖線）
◇　想像線　　（２点鎖線）
◇　寸法線　　（実線）

次に、寸法の書き方。

◇　単位は mm。でも、「mm」は書かない。
◇　寸法記号は、
　　　・ 厚さ　t　　　　　　　　 thickness
　　　・ 半径　R　　　　　　　　radius
　　　・ 面取り　C　　　　　　　Chamfer
　　　・ 円柱　Φ　　　　　　　「マル」と読む
　　　・ 角柱（正四角柱）　□　「カク」と読む

 ではここで、線の名称と寸法表示の意味を確認しながら、練習問題をやってみましょう。

---

《 答え 》
　　(1)　かくれ　　(2)　中心　　(3)　50　　(4)　48　　(5)　20
　　(6)　寸法　　(7)　想像　　(8)　外形　　(9)　110

車のおもちゃと収納棚を製図する

◇　目的・機能（使う場所、使いやすさ、デザイン）を考える。
◇　構造・材料（丈夫さ、材料費）を選ぶ。
◇　製図（ラフなスケッチから具体的で詳細な設計図へ）する。
◇　製作（材料入手→加工→組み立て→仕上げ）する。

これらをひっくるめて「設計」といいます。ところで、授業でやるのは「製図」までです。製作は省略します。

　さて、製図のきまりに従って、製図してみましょう。お題は「車のおもちゃ」と「収納棚」の２つ。
　自由に考えてくれていいですが、あまり複雑なものを作ろうとするときりがないので、
ある程度シンプルなもので結構です。でも、お約束として、

◇　キャビネット図または等角図のどちらか一方を描く。
◇　投影図を描く。
◇　寸法を入れる。

ことは守ってください。なお「車のおもちゃ」では最低１ヶ所の
面取り（平面または円形に）を入れてください。
　また、タイヤが動かなくてもかまいません。（タイヤが動くようなものは難しい）
　「収納棚」では多少の力が加わっても壊れないような丈夫なもの
を製図してください。

---

　一輪車みたいなものでも、リアルにやろうとすると寸法を全部確定して表示するのは難しい。だから、シンプルなおもちゃでいいんです。それでもいろいろ決めなきゃいけないことはありますから。
　また、前の課題で中が詰まったものだけを描いたので、厚さを無視して見取り図を描く生徒が何人かいた。けれどもそれじゃぁ板の厚さも強度もゼロになっちゃって、そんな収納棚を作れるわけがありません。

　まぁ頑張ってやってください。この課題にあてる時間は３時間。３時間で２つの課題を仕上げてもらいます。以上、製図の基本練習と合わせてのべ５時間で、製図の授業の中学生バージョン、完了です。

角柱２本の交わり

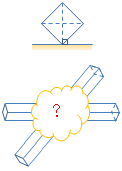
断面が正方形である角柱が２つあって、床面に対して右図のように置いてあります。
　２つの角柱が垂直に交わっているとき、重なっている部分はどんな立体でしょうか？

　見取り図を描いてみましょう。まず投影図を、続いてキャビネット図を描くのがいいでしょう。
 　あわせて、その立体の体積を、正方形の対角線の長さを 1 として求めてください。

---

　　　　　　　（投影図）　　→　　 （俯瞰図）　→　　 （キャビネット図）

　この立体は八面体になりますが、正八面体とは微妙に違って、正八面体を高さ方向に少し縮めた形です。
　また、この立体が四角すいを２つ重ねたものであることを利用して、体積は 1/ 3 です。

※ 続いて、角柱をもう１本加えて「角柱３本の交わり」について考えます。

角柱２本　→　円柱２本　→　角柱３本　→　円柱３本

円柱２本の交わり

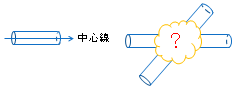
円柱が２つあって、中心線が垂直に交わっています。
　２つの円柱が重なっている部分はどんな立体でしょうか？

　見取り図を描いてみましょう。まず投影図を、続いてキャビネット図を描くのがいいでしょう。
　あわせて、その立体の体積を、底面の円の半径を 1 として求めてください。

---

　　この立体を横から見ると ○ ですが、上から見ると、□ の中に × が見えます。
　　そのことを考えてキャビネット図を描くと、下中図のようになります。

　　　　　　　 （投影図）　　→　　（キャビネット図）　　→　　（体積）

　次に、体積を求めてみましょう。高校数学でやった積分を使えば求められます。
　鉛直方向に軸をとって、軸に垂直な平面でこの立体を切ると、切り口は正方形になります。
　その辺の長さは 2√1-t² ですから、断面積は S(t)＝4(1-t²)　で、これを −1 から 1 まで積分すれば完成です。

※ 続いて、円柱をもう１本加えて「円柱３本の交わり」について考えます。

角柱２本　→　円柱２本　→　角柱３本　→　円柱３本

角柱３本の交わり

　前の問題「角柱２本の交わり」で、角柱２本が垂直に交わるときの交わり部分について考えました。

　では、さらにもう１つ角柱を加えて、角柱３本が垂直に交わるときの交わりについて考えましょう。
　どんな形？　体積は？

---

角柱２本の交わり は右のような八面体で、底面の対角線の長さが 1 のときの体積は 1/3 でした。
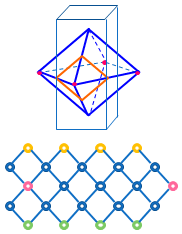
　ここに３本目の角柱を突き通すと、八面体の辺の中点を通って、４ヶ所を切り落とすことになります。

　切り落とす１ヶ所の体積は、相似比を考えて、八面体の 1/16 ですから、残った部分の体積は　1/3×（1－4/16）＝ 1/4　です。
　これが、角柱３本の交わりの体積です。

　ところでこの立体は、右のような骨組みの同じ色の点をつないでできる立体と同じです。右図の辺はどれも同じ長さですが、これを立体として組み立てると、上下の８つの四角形が縦に伸びて、中ほどの４つの四角形が横に伸びて、すべてが合同なひし形になります。
　これを「ひし形１２面体」と呼びます。正多面体ではありませんが。

角柱２本　→　円柱２本　→　角柱３本　→　円柱３本

円柱３本の交わり

　前の問題「円柱２本の交わり」で、円柱２本（の中心線）が垂直に交わるときの交わり部分について考えました。

　今日は、さらにもう１つ円柱を加えて、円柱３本が垂直に交わるときの交わりについて考えましょう。
　どんな形？　体積は？

---

　円柱２本の交わりはこの（↓）ようなものでした。

　これをもう１つの円柱で切ると、上と下はそのままで、中ほどの回りの部分が（↑）削り取られます。
　ここで、削られずに上に残った部分を Ａ と呼ぶことにします。Ａ の体積は、円柱２本の交わりを求めたときと同じやり方で積分で求められます。
　また対照性を考えると、円柱３つの交わりの図形は、立方体の６面に Ａ がくっついたものになります。
　というわけで、その体積は上の計算を実行して、 8 (2-√2)　となります。

角柱２本　→　円柱２本　→　角柱３本　→　円柱３本

直線と平面の位置関係

　カリキュラム「製図」の高校生バージョンはもう少し続きます。ここでちょっと頭の体操。

☆　ℓ , ｍ , ｎ は直線、 α , β , γ は平面である。次の命題が真なら 1 を、偽なら 0 を記入しよう。

(1)　ℓ ∥ｍ　,　ℓ ∥ｎ　　⇒　　 ｍ∥ｎ
(2)　ℓ ⊥ｍ　,　ℓ ⊥ｎ　　⇒　　 ｍ⊥ｎ
(3)　ℓ ⊥α　,　ℓ ⊥b　　 ⇒　　 α∥β
(4)　ℓ ⊥α　,　m⊥α　 　⇒　　 ℓ ∥m
(5)　α⊥β　,　α⊥γ　　  ⇒　　 β∥γ

※ 情報科の授業っぽく、1 と 0 の２進法仕様で真偽を表記します。
※ ℓ ⊥ｍ は、ℓ と ｍ が交わっていなくてもかまいません。
　平行移動して直角に交わるなら ⊥（垂直）です。

---

《答え》　　順に、　1　0　1　1　0

　　（反例）　(2)　　　　　　　　　　　　　　　　　　(5)

　さて、次の課題は、上の（反例）に示した程度のスケッチをすることです。あと 10 個ほど描いて完了です。

空間図形を描く（その１）

　製図の練習をある程度積んだところで、高校数学の空間図形・空間ベクトルと関連付けてスケッチします。
　ここでの目的は、数学の空間図形の問題を考えるために、空間図形を把握することです。ですから、製図の描き方のルールにとらわれず、それっぽく見える図を描ければよいこととします。
　ところで、まず確認したいのは空間図形を正確に紙に描くのは無理だということです。
それを承知の上で、それっぽくウソを描くしかありません。さて、まず基本図形の描き方。
　直線や平面は無限に伸びるものですが、そんなものをそのまま紙に描けるはずがありません。
　また、球と円を区別して描かなければなりません。というわけで、次のように描きましょう。

　　　　　　　　　　　　直線　　　　平面　　　球　　　 円

　　　　　　　　　　　 線分  　　 平行四辺形  　 円 　　 だ円 

それから、見取り図の中に式を立てるのに使える情報も盛り込みたいですね。数学の問題を解くには、そこがポイントです。では、課題です。

(1)　平行でない２平面 α , β の交線 ℓ
(2)　点 A を通り、平面 ABC に垂直な直線 ℓ
(3)　ねじれの位置にある２直線 ℓ , m の両方に直交する直線 n
(4)　球面 C と平面 α の交円 D
(5)　点 A を通り、球面 C に接する直線群（曲面π）ならびに接点群（曲線 D）

---

　見取り図を描くのと合わせて、直角になるところには直角記号を入れておきたいですね。そうすれば「垂直 ⇔ 内積ゼロ」を使って式を立てたり、「三平方定理」 使って長さを求めたりできますから。

空間図形を描く（その２）

　前回に続いて、もうちょっと複雑なもの（おもしろいもの）を描いてみましょう。
　数学の空間図形の問題でよく出てくるものですが、いきなり計算しようとせず、まず位置関係をつかみましょう。

(1)　２点 A , B が平面αに関して同じ側にあるとき、
　　「AP＋BP が最小となるような平面α上の点 P」

(2)　２点 A , B が直線 ℓ 上にないとき、
　　「△ABP の面積が最小となるような直線 ℓ 上の点 P」

(3)　直線 m の周りに直線 ℓ を回転してできる回転体

(4)　円すい曲面（２つの円すい）を平面で切ったときの切り口が、
　　放物線（だ円、双曲線）になる

(5)　光源 A から発した光が、中心が z 軸上にある球に当たって、
　　その影が xy 平面上の放物線を描く

---

　まずはじめに (4) に関連する（というより、そのまんまですが）話を少々。円すい曲面を平面で切るとき、

　　　　　　　　　母線に平行　　　もっと寝かせる　　もっと立てる

　　　　　　　　　　　↓　　　　　　　　↓　　　　　　　　↓
　　　　　　　　　　放物線　　　　　　 だ円　　　　　　　双曲線

となります。放物線・だ円・双曲線をあわせて２次曲線と呼びますが、「円すいを平面で切ると、切り口は２次曲線になる」ということです。(5) はこのことをふまえて考えてください。

(1)　２点 A , B が平面αに関して同じ側にあるとき、
　　「AP＋BP が最小となるような平面α上の点 P」
→　αに関してAと対称な点を A' とすると、AP＋PB＝ A’P＋PB
　　これが最小になるのは、A’, P , B が一直線上にあるとき。

(2)　２点 A , B が直線 ℓ 上にないとき、
　　「△ABP の面積が最小となるような直線 ℓ 上の点 P」
→　AB の長さは変わらないから、
　　三角形の高さが最小になるときを考えればよい。

(3)　直線 m の周りに直線 ℓ を回転してできる回転体
→　つづみ形になる。
　　体積を求めるには、回転軸に沿って積分すればよい。
　　回転軸を通る平面でこの曲面を切ると、双曲線になる。

(4)　円すい曲面（２つの円すい）を平面で切ったときの
　　切り口が、放物線（だ円、双曲線）になる
→　母線に平行な平面で切ると、放物線。
　　　　もっと寝かせると、だ円。
　　　　もっと立てると、双曲線。

(5)　光源 A から発した光が、中心が z 軸上にある球に
　　当たって、その影が xy 平面上の放物線を描く

→　円すい（球の影）を平面（xy 平面）で切るのと同じこと。
　　切り口が放物線だということは、直線ℓと xy 平面は平行。

　高校数学のことをイメージしながらいろいろ語りましたが、これは情報科のカリキュラムなので、メインテーマはあくまでもお絵かきです。

　以上で「製図」の授業の高校生バージョン、完了です。

◎ エネルギーについて考える

情報科の教材「エネルギーについて考える」の《テーマ》は10個。
１．石油　　　　２．石炭　　　　３．水力　　　　４．原子力　　　５．地熱
６．太陽光　　　７．風力　　　　８．バイオ　　　９．エコカー　　10．地球温暖化

プレゼンのために作るスライドは全部で６枚。
＜スライド１＞　テーマと氏名を大きくはっきりと書く。
＜スライド２＞　ネットから関連する統計データを探して、表を作りグラフ化する。
＜スライド３＞　前のスライドで引用した統計を分析して、そこから読み取れることを書く。
＜スライド４＞　発電の仕組みや原理など。あるいは、そのエネルギーの特性。
＜スライド５＞　その発電のメリットとデメリットをそれぞれ３つずつ挙げる。
＜スライド６＞　考えたり議論したりする際の論点・焦点を、自分の問題意識に沿って提案する。

流れ	時間	内容
資料作成	6	説明のポイント
		資料作成のツボ
		サンプル
グループ作業	2	グループ作業
	2	発表

　授業時間は 10 時間としましたが、グループ作業の部分を膨らませたり削ったりすることは可能でしょう。

説明のポイント　→　資料作成のツボ　→　サンプル　→　グループ作業　→　発表

エネルギーについて考える（説明のポイント）

情報科の教材「エネルギーについて考える」の《テーマ》は10個。
１．石油　　　　２．石炭　　　　３．水力　　　　４．原子力　　　５．地熱
６．太陽光　　　７．風力　　　　８．バイオ　　　９．エコカー　　１０．地球温暖化

この中の１つを生徒に与えますが、生徒に自由に選ばせたりはしません。
　　◇　出席番号が1番・11番・21番・31番の生徒にはテーマ「石油」を、
　　◇　出席番号が2番・12番・22番・32番の生徒にはテーマ「石炭」を、
　　　　　　　・・・
　　◇　出席番号が10番・20番・30番・40番の生徒にはテーマ「地球温暖化」を与えます。
　生徒が自力でできるように、同じテーマの人が席の近くにならないようにとの配慮によるものです。

プレゼンのために作るスライドは全部で６枚。
＜スライド１＞　テーマと氏名を大きくはっきりと書く。
＜スライド２＞　ネットから関連する統計データを探して、表を作りグラフ化する。
＜スライド３＞　前のスライドで引用した統計を分析して、そこから読み取れることを書く。
＜スライド４＞　発電の仕組みや原理など。あるいは、そのエネルギーの特性。
＜スライド５＞　その発電のメリットとデメリットをそれぞれ３つずつ挙げる。
＜スライド６＞　考えたり議論したりする際の論点・焦点を、自分の問題意識に沿って提案する。

---

　＜スライド１＞のテーマは与えられたテーマからもっと絞り込んだテーマが望ましい。たとえば「原子力」というだけではまだまだ広すぎる。もっと論点・焦点を絞り込みたい。コストについてなのか、安全性についてなのか、資源量についてなのかなど。

　＜スライド２＞では、ネットからグラフになってるもの（画像ファイル）をコピペするのはダメ。表になってるもの（１次データ）を探して、自分で数値を入力してグラフ化するのがお約束。
　１次データを探しやすいのは「総務省統計局」のサイトです。とはいえ、そのサイトは日本国内のデータが充実している一方で、世界のデータはちょっと弱い。英文を読む気力があるなら、ＯＥＣＤやＩＭＦ、国連などのサイトが使えそうです。

　＜スライド４＞では図解して示すとわかりやすいでしょう。文章でダラダラ書くのは、パワポの使い方としてうまくない。せめて箇条書きにしてね。
　つまり、ここでもやっぱりコピペできないってこと。自分で編集するしかないわけだ。

　＜スライド５＞ではメリットとデメリットとを３つずつ挙げるのがお約束。そうすることで問題の本質が見えてくる。メリットが無いならそのエネルギー資源は要らないはずだし、デメリットが無いなら他のエネルギー資源は要らないはずだから。

---

　授業１時間目。以上のことを説明すると、生徒からいろんな声が上がりました。

◇ 「原子力」の生徒から「核兵器でもいい？」と。
　　→　それには「メリットとデメリット、３つずつ挙げてね」と。
◇ 「地熱」の生徒から「温泉は？」と。
　　→　それには「『肩こりに効く』なんてのは要らないよ」と。
◇ 「エコカー」の生徒から「子ども店長は？」と。
　　→　それには「データ探して、グラフ作ってね」と。

６枚のスライドに書くべきことがきちんと書かれていて、一貫性があればまぁ何でもいいわけです。
　出だし好調、我ながら「なかなかいい課題だなぁ」という実感です。

説明のポイント　→　資料作成のツボ　→　サンプル　→　グループ作業　→　発表

エネルギーについて考える（資料作成のツボ）

情報科の教材「エネルギーについて考える」の《テーマ》は10個。
１．石油　　　　２．石炭　　　　３．水力　　　　４．原子力　　　５．地熱
６．太陽光　　　７．風力　　　　８．バイオ　　　９．エコカー　　１０．地球温暖化

プレゼンのために作るスライドは全部で６枚。
＜スライド１＞　テーマと氏名を大きくはっきりと書く。
＜スライド２＞　ネットから関連する統計データを探して、表を作りグラフ化する。
＜スライド３＞　前のスライドで引用した統計を分析して、そこから読み取れることを書く。
＜スライド４＞　発電の仕組みや原理など。あるいは、そのエネルギーの特性。
＜スライド５＞　その発電のメリットとデメリットをそれぞれ３つずつ挙げる。
＜スライド６＞　考えたり議論したりする際の論点・焦点を、自分の問題意識に沿って提案する。

---

　さて、上記10個のテーマはそれでもかなり広いんです。それをさらに絞って、自分で考えるときの焦点、他人と議論するときの論点を提出するのが＜スライド６＞です。

○ 環境負荷、○ コスト、○ 資源量、○ 安全性、○ 将来性、○ 自作するなら、

など観点はいくらでもあります。それを全部盛り込もうとすると、言いたいことがはっきりしない、焦点のボケたプレゼンテーションになってしまう。それじゃぁ発表する人も聴く人もあまり面白くないんですね。

６枚のスライドのうち、もっとも大事なのは＜スライド６＞の「論点・焦点」です。それを支えるのは、各自の興味・関心であり、問題意識です。
　本来は、それがまずあって、そこに集約するように「データ→分析」と「仕組み・特性」と「メリット・デメリット」を選ぶべきです。そして、最後に＜スライド１＞の「タイトル」が決まる。これが理想形です。
　＜スライド１＞から順番に作っていくと、「データ → 分析」と「仕組み・特性」と「メリット・デメリット」がまるで別方向を向いて、最後の＜スライド６＞に行き着いたときには何も書けなくなってしまうでしょう。

説明のポイント　→　資料作成のツボ　→　サンプル　→　グループ作業　→　発表

エネルギーについて考える（サンプル）

情報科の教材「エネルギーについて考える」の《テーマ》は10個。
１．石油　　　　２．石炭　　　　３．水力　　　　４．原子力　　　５．地熱
６．太陽光　　　７．風力　　　　８．バイオ　　　９．エコカー　　１０．地球温暖化

プレゼンのために作るスライドは全部で６枚。
＜スライド１＞　テーマと氏名を大きくはっきりと書く。
＜スライド２＞　ネットから関連する統計データを探して、表を作りグラフ化する。
＜スライド３＞　前のスライドで引用した統計を分析して、そこから読み取れることを書く。
＜スライド４＞　発電の仕組みや原理など。あるいは、そのエネルギーの特性。
＜スライド５＞　その発電のメリットとデメリットをそれぞれ３つずつ挙げる。
＜スライド６＞　考えたり議論したりする際の論点・焦点を、自分の問題意識に沿って提案する。

---

　生徒に見せるためのサンプルを作ってみた。

　サンプルにしちゃちょっとインパクト強すぎでしょうか。

説明のポイント　→　資料作成のツボ　→　サンプル　→　グループ作業　→　発表

エネルギーについて考える（グループ作業）

情報科の教材「エネルギーについて考える」の《テーマ》は10個。
１．石油　　　　２．石炭　　　　３．水力　　　　４．原子力　　　５．地熱
６．太陽光　　　７．風力　　　　８．バイオ　　　９．エコカー　　１０．地球温暖化

授業時間はのべ10時間。

◇　個人でプレゼン資料作成（拡散しがちな論点・焦点を絞り込む）（６時間）

◇　同じテーマの人が集まって、発表の準備（合体、いいとこどり、どれか１つを選ぶ…）（２時間）

◇　グループで発表（白熱教室になるかも？）（２時間）

---

　さて、これまで６時間かけて個人のプレゼン資料を作成して、提出したところです。

　そして今日からグループ活動。「さて、どうやったらいいものか？」と方針が定まらないままむかえたが、やってみた結果（と反省）を踏まえて現時点でのベターと思えるやり方を示してみる。

《グループ活動１時間目前半》

◇　前回提出したパワポファイルに各ＰＣからアクセスできるようにあらかじめ仕込んでおく。

◇　グループで１台のＰＣを起動して、グループ内でお互いにプレゼンし合う。（各自5分程度）

　　（全員分を起動すると、他人のプレゼンを聞かずに、自分の資料作成に専念する生徒が現れるだろうから）

《グループ活動１時間目後半》

◇　発表に向けて相談。（何を発表するか？誰が何を担当するか？）

◇　自分のプレゼン資料を１枚ずつプリントアウトして、紙の上でプレゼン資料を修正。

　　（自分でやってみれば、また他人のを聞いてみれば、気づくことはいろいろある）

《グループ活動２時間目》

◇　グループで発表する内容と役割分担を確定する。

◇　グループで１台のＰＣを起動して、発表のための資料作成。

　　（時間のことを考えると、誰かの資料をベースにして、それに手を加えるのが現実的だろう）

説明のポイント　→　資料作成のツボ　→　サンプル　→　グループ作業　→　発表

エネルギーについて考える（発表）

情報科の教材「エネルギーについて考える」の《テーマ》は10個。
１．石油　　　　２．石炭　　　　３．水力　　　　４．原子力　　　５．地熱
６．太陽光　　　７．風力　　　　８．バイオ　　　９．エコカー　　１０．地球温暖化

プレゼンのために作るスライドは全部で６枚。
＜スライド１＞　テーマと氏名を大きくはっきりと書く。
＜スライド２＞　ネットから関連する統計データを探して、表を作りグラフ化する。
＜スライド３＞　前のスライドで引用した統計を分析して、そこから読み取れることを書く。
＜スライド４＞　発電の仕組みや原理など。あるいは、そのエネルギーの特性。
＜スライド５＞　その発電のメリットとデメリットをそれぞれ３つずつ挙げる。
＜スライド６＞　考えたり議論したりする際の論点・焦点を、自分の問題意識に沿って提案する。

---

　これまで６時間かけて各人でプレゼン資料を作成し、２時間かけてグループで発表の準備をしてきました。今日はグループによる発表の１時間目。１班「石油」から６班「太陽光」まで発表しました。各班の発表の時間は５分間。そのあと聞き手からの質疑を受けました。
　時間の関係で各班につき１つか２つの質疑しか受けられないのですが、なかなか手ごわい質疑が連発でした。

◇「石油の○○と△△」というタイトルで発表した１班に対しては、
→　で、結局、○○と△△には何が入るんですか？

◇「石炭の将来性」を考えた２班に対しては、
→　「石炭を使え」なのか「使うな」なのか、どっちを言いたいんですか？

◇「太陽光パネルの普及」のグラフを提示した６班に対しては、
→　グラフの縦軸の単位はなんですか？

プレゼンテーターはたじたじ。発表する側も聞く側も良い経験が出来たと思います。

説明のポイント　→　資料作成のツボ　→　サンプル　→　グループ作業　→　発表

エクセルで九九の表を作る

【問】エクセルの１行目のセルに１つずつ、左から順に１,２,３,…,９が並んでいます。同じくＡ列のセルにも１つずつ、上から順に１,２,３,…,９が並んでいます。
　さて、セルB2に関数式を入力して、そこからセルJ2まで右方向にコピーして、さらにセルJ10まで下方向にコピーして、掛け算の九九の表を作りたい。セルB2にどんな関数式を入れればいいでしょうか？

　　　　　　　Ａ列目
　　　　　　　　↓
　　１行目→　　　1　　2　　3　　…　　9
　　　　　　　　1　？　　→　　→　　→
　　　　　　　　2　　　　　　　　　　　　↓
　　　　　　　　3　　　　　　　　　　　　↓
　　　　　　　　　　　　　…
　　　　　　　　9　　　　　　　　　　　　↓

　くれぐれも、関数式を直接入力するのは、セルB2だけです。他のセルの関数式は、セルB2の式をコピーして仕上げてください。
　次の[選択肢]ア～タから1つ選んでください。

[選択肢]　ア　＝A2*B1　　　イ　＝A2*B$1　　　  ウ　＝A2*$B1　　　エ　＝A2*$B$1
　　　　　オ　＝A$2*B1　　 カ　＝A$2*B$1　　　キ　＝A$2*$B1　　ク　＝A$2*$B$1
　　　　　ケ　＝$A2*B1　　 コ　＝$A2*B$1　　　サ　＝$A2*$B1　　 シ　＝$A2*$B$1
　　　　　ス　＝$A$2*B1　　セ　＝$A$2*B$1　　ソ　＝$A$2*$B1　　タ　＝$A$2*$B$1

---

　エクセル関数の「相対参照・絶対参照」の問題です。エクセルの実習課題としてもいけます。
　＄マークをどこにつけるかがポイントです。候補は４か所あって、それらの場所に＄マークをつけてもつけなくてもセルB2の表示は同じですが、右方向・下方向にコピーすると、コピーした先のセルでは＄マークがあるかないかで表示が変わってきます。
　正解は「コ」です。右方向・下方向にコピーして一発で正しく九九の表ができるのは、これだけです。ついでながら、次のような問題を付け加えることもできます。

○　セルK2に関数式「= SUM(B$2:J2)」を入力すると、セルK2の値は（チ）となる。
　　次に、セルK2からK10まで下方向にコピーすると、セルK10の値は（ツ）となる。

　これは「関数式の意味が分かっているか、関数式をコピーしたときの式の変化が分かるか」を問う問題です。値を求めるには、まともに計算してもいいですが、工夫するとより簡単に計算できます。答えは、
　　チ　→　1+2+3+…+9＝45
　　ツ　→　(1+2+3+…+9)(1+2+3+…+9)＝45×45＝2025
となります。

入試の合否判定

　いまさらですが、○○中学合格おめでとうございます。ちょっと気が早いですが、○年後には大学受験ですね。よい結果を期待しています。さて、今日は入試の合否判定の現場を覗いてみることにしましょう。次の空欄①～⑦に関数式（または関数式の一部）を入れなさい。ただし、下方向にコピーして正しく動く式を答えること。

	A	B	C	D	E	F
1	ボーダー				点
2	受験番号	科目Ａ	科目Ｂ	合計	合否	補欠
3	１	73	88
4	2	61	70
5	3	91	52
：	：	：	：

(1)　まず、D列に科目Ａと科目Ｂの合計点を表示します。セルD3の式は（ ① ）です。

(2)　セルD1にボーダーの点数を入力します。科目Ａと科目Ｂの合計点がセルD1の値以上であればE列に「合」の文字を表示し、そうでなければ何も表示しないようにするには、セルE3の式を（ ② ）とします。

　続けて、補欠合格について考えましょう。ボーダーより１点低い者を「第１補欠」、２点低い者を「第２補欠」、３点低い者を「第３補欠」とし、それぞれを数字の 1 , 2 , 3 でF列に表示することにしましょう（それ以外は空欄とします）。セルF3の式を次のようにすればそれが可能です。
　　　　=IF(③,””,IF(④,””,⑤))

(3)　ところで、実際の入試では他の合否基準を採用する場合もあります。

《例１：一芸入試》
科目Ａ,Ｂのうち少なくとも一方が90点以上であればE列に「合」の文字を表示し、それ以外は何も表示しないようにするには、セルE3の式を次のようにすればよい。
　　　　=IF(⑥,”合”,””)

《例２：足切り》
合計がセルD1の値以上で、かつ科目Ｂの得点が50点以上であればE列に「合」を表示し、それ以外は何も表示しないようにするには、セルE3の式を（⑦）とします。

---

中１から中２の２学期までに習ったエクセル関数は、

＜四則計算＞　＋,－,＊,／
＜基本関数＞　=SUM(セル範囲)　　=AVERAGE(セル範囲)
　　　　　　　=MAX(セル範囲)　　=MIN(セル範囲)　　=COUNT(セル範囲)
＜条件分岐＞　=IF(条件式,真の場合,偽の場合)
＜相対参照と絶対参照＞　A1,$A1,A$1,$A$1

これだけです。これだけで設問のようなことが実現できます。

《解答》
(1)　D3　①　=B3+C3　または　=SUM(B3:C3)
(2)　E3　②　=IF(D3>=D$1,"合","")
　　 F3　③　D3>=D$1　　④　D3<D$1–3　　⑤　D$1–D3
(3)　E3　⑥　MAX(B3:C3)>=90
　　 E3　⑦　=IF(D3>=D$1,IF(C3>=50,"合",""),"")

真理表の限界

【問】条件式が２つ（Ｐ, Ｑとする）あるとき、その真偽の組み合わせは全部で4通りあります。だから、ある論理式の真偽を判定するための表を作ると（タイトル行を除いて）4行必要です。また、その２つの原子式から作られる論理式の真偽の組み合わせは、次表のように全部で16通りあります。

　　Ｐ　Ｑ　｜　ア　イ　　　Ｐ　ウ　Ｑ　　　エ　　　　　　　　　オ　　　　　カ
　　ー　ー　┼　ー　ー　ー　ー　ー　ー　ー　ー　ー　ー　ー　ー　ー　ー　ー　ー
　　１　１　｜　１　１　１　１　１　１　１　１　０　０　０　０　０　０　０　０
　　１　０　｜　１　１　１　１　０　０　０　０　１　１　１　１　０　０　０　０
　　０　１　｜　１　１　０　０　１　１　０　０　１　１　０　０　１　１　０　０
　　０　０　｜　１　０　１　０　１　０　１　０　１　０　１　０　１　０　１　０

(1)　表中の ア , カ にあたる論理式を何というか。その名称を答えなさい。

(2)　イ , ウ , エ , オ にあたる論理式を１つずつ、Ｐ , Ｑ の両方または片方を用いて書きなさい。

(3)　授業で扱った真偽判定法は、頭からっぽで 0 と 1 を書き込むだけでいいので簡単で便利だが、弱点もある。それは原子式が多くなると、表がとても大きくなることだ。
　たとえば原子式が P , Q , R の３つある場合は行の数は（タイトル行を除いて）全部で（ ① ）行必要になり、３つの原子式から作られる論理式の真偽の組み合わせは全部で（ ② ）通りになる。
　また、原子式が P , Q , R , S , T の５つある場合は行の数は（タイトル行を除いて）全部で（ ③ ）行必要になり、５つの原子式から作られる論理式の真偽の組み合わせは全部で約（ ④ ）億通りになる。
　こうなると、とても書ききれない。ましてや「すべての x において」のようなものを扱うことはまったく不可能だ。
　ではそれらを扱うにはどうすればいいかというと、やり方をまるで変えなければならなくなる。続きは大学で、もしくは自学自習でやってください。

---

《正解例》は、次の通りです。

(1)　ア：トートロジー（恒真式）　　カ：矛盾式（恒偽式）
　　　　※ トートロジーの否定は矛盾式に、矛盾式の否定はトートロジーになる。
(2)　イ：Ｐ∨Ｑ　　ウ：Ｐ⇒Ｑ　　エ：Ｐ∧Ｑ　　オ：Ｐ（Ｐでない、Ｐの上にバーをつけて表す）
　　　　※ 複雑なものを作ろうとすれば他にも答えは無限にあるが、重要かつ頻出かつシンプルなものは上の通り。
　　　　　 表中 イ , ウ , エ , オ の値（１か０か）が「∧ , ∨ , ⇒ , バー」の定義にあたります。

(3)　①　2³ ＝ 8 　　　②　2⁸ ＝ 256 　　　③　2⁵ ＝ 32 　　　④　2³² ＝ 40 億　
　　　※　２のｎ乗の簡易計算法は こちら をどうぞ。

人口ピラミッドの作り方

　先の見えない時代と言いますが、はっきりくっきり見えている未来もあります。
　たとえば「20年後の人口ピラミッド」。20年後の勤労世代は今現在生まれている人たちですからこれ以上増えようがありませんし、高齢者が減る見込みもありません（計画的に減らすことはできない）。仮にこれから出生率が急上昇しても、これから生まれてくる人たちは20年後にはまだ子供ですから、そうなったら勤労世代の負担はますます増えるばかり。20年後なんてすぐですよ。

　それでは実際に20年後の人口ピラミッドを作ってみましょう。将来の人口ピラミッドは、直近の２回の国勢調査（2010年と2015年）のデータから作れます。国勢調査は5年に一度行われます。人口ピラミッドは男女別に通常5歳刻みで表します。これには訳があって、たとえばある時の国勢調査で50〜54歳だった人は次の国勢調査の時には55〜59歳になっていますから、そのグループの人口を比較することで各年齢区分の5年間での生存率（死亡率）がわかるわけです（もちろん出入国の数も影響しますが、その割合は比較的小さい）。もう一つ必要なデータは出生率で、将来の出生数を算出するには、その時点での出産年齢の女性の数も関係します（合計特殊出生率の計算では「15〜49歳の女性」を出産年齢としています）。これは直近の１回の国勢調査の結果から算出できます。
　こうして過去２回の国勢調査の結果から出生率と各年齢区分の生存率（死亡率）を求めて、それがこれからも変わらないと想定すれば５年後の人口ピラミッドが作れます。この操作を繰り返すことで10年後、15年後、20年後の人口ピラミッドも作れるわけです。

◇　2010年時点で50〜54歳のグループの5年間の生存率は「E15/C14」ですから、セルG15の関数式は「=E15/C14*E14」です。セル範囲E5：F24に関数式をコピーしてください。

◇　2010〜2015の5年間の出生率を「E4/SUM(F7:F13)」とすると、セルG4の関数式は「=E4/SUM(F7:F13)*SUM(H7:H13)」となります。セルH4も同様です。

◇　セルG25は合計ですから「=SUM(G4:G24)」、これを右方向に１つコピーしてください。

◇　続いてG列とH列をまとめてI列以降にコピーすれば、10年後、15年後、20年後の年齢区分別人口の表が作れます。

続いて、人口ピラミッドのグラフを作ってみましょう。下のグラフが先ほどの手順で作った「20年後（2035年）の人口ピラミッド」です。政府発表のものとほぼ同じです。

　エクセルで人口ピラミッドのグラフを作るにはいろんな方法がありますが、最も簡単な方法を紹介しましょう。

◇　まず男性の数だけ、あらかじめ -1 をかけて負の数にしておきます。

◇　次に「挿入」リボンの「グラフ」の中の「おすすめグラフ」をクリックします。その中の「積み上げ横棒」を選べば、ほぼ完成です。

◇　そのままでも良いのですが、年齢区分の表示がグラフの中央にきてしまって読みにくい。それを解消するために上のグラフでは年齢区分の表示を左端に寄せました。もっと簡単に、年齢区分の表示を消してしまうという手もあります。

みなさんも将来の日本の人口ピラミッドを見たことがあるでしょうけれど、自分で計算して作ってみると、やっぱり気づくことはいろいろあります。それは「将来の予想」と言うより、ほぼ「確実な未来」なのです。

　最後に、今回の話題に関連する便利なサイトと興味深い施設を紹介しましょう。まず便利なサイトは「Population Pyramids of the World」（→ http://populationpyramid.net/ ）です。国と年をクリックして選べば、その時点での人口ピラミッドを描いてくれます。
　興味深い施設とは、総務省統計局の建物内部にある「統計資料館」です。東京都新宿区にあります。この資料館の見所は、大正時代に行われた第１回国勢調査のポスターなど。私が行ってレポートにまとめました（→ https://omori55.blogspot.com/2019/03/blog-post_959.html ）ので、よろしければご覧ください。

駅伝の記録集計（エクセル）

《エクセル問題》
　今日は絶好の駅伝日和である。まもなく最終区間の走者がゴールする。
　下表は最終走者の成績の集計表である。セルF2～F31には最終中継所から送られてきた通過タイムがすでに入力してある。セルB2～C31にゴールした順にチーム番号とゴールタイムを入力したときに、セルG2～J31に各チームのゴールタイム、最終走者の区間記録（所要時間）、区間順位、ならびに区間賞（１位の者だけに「区間賞」と表示する）を表示するようにしたい。
　セルC2～C31とF2～H31の書式は「時間形式」であるとする。セル G2 , H2 , I2 , J2 に入る式を答えよ。ただし、それぞれ下方向にコピーして正しく動くような式を答えること。

	A	B	C	D	E	F	G	H	I	J
1	ゴール 順位	チーム 番号	ゴール タイム		チーム 番号	通過 タイム	ゴール タイム	区間 記録	区間 順位	区間 賞
2	1				101	1:15:42
3	2				102	1:09:27
4	3				103	1:20:59
：	：				：	：
31	30				130	1:10:13

※「通過タイム」＝第１走者がスタートしてから最終走者がタスキを受け取るまでの通算時間
　「ゴールタイム」＝第１走者がスタートしてから最終走者がゴールするまでの通算時間

《授業で扱った関数一覧》

四則計算
＄マークの使い方（相対参照と絶対参照）
基本関数５つ（SUM,AVERAGE,COUNT,MAX,MIN）→書式はいずれも=SUM(セル範囲)
=IF(条件式,真の場合,偽の場合)
=ROUND(数値,桁数)
=COUNTIF(セル範囲,検索条件)
=RANK(数値,セル範囲,順序)
=VLOOKUP(検索値,セル範囲,列番号,検索の型)

※試験問題の中でも、関数とパラメータについて再度説明しています。

---

《正解》

G2　=VLOOKUP(E2,B$2:C$31,2,0)

H2　=G2–F2

I2　=RANK(H2,H$2:H$31,1)

J2　=IF(I2=1,"区間賞","")

※正解は他にもあります。エクセルに入力したときに、正しく動けば ○ です。

パスカルの三角形の裏事情

　パスカルの三角形を書けば (a+b)ⁿ の展開式の各項の係数を簡単に求めることができる。たとえば、
 　　　　　(a+b)⁵ ＝ a⁵ ＋ 5a⁴b ＋ 10a³b² ＋ 10a²b³ ＋ 5ab⁴ ＋ b⁵　　という具合である。
 　パスカルの三角形の書き方は、
 　　　　　各段両端は 1 。
 　　　　　上段の２数の和を、２数の真ん中下段に書く。
 　　　　　これを繰り返す。
これだけである。上から n 段目の数が (a+b)ⁿ の展開式の各項の係数というわけである。
 　さて、今日は「なぜそれでうまくいくのか」を考えよう。

１．パスカルの三角形の中の数は、元をただせば「(a＋b)ⁿ の展開式の a^n－r b^r の係数 _nC_r 」である。
 　　∵）　(a＋b)ⁿ＝(a＋b)(a＋b)…(a＋b)
　　　　　n 個の（a＋b）から a か b のどちらかを取る。
　　　　　n 個のうち b をちょうど r 個取る場合の数は _nC_r 通り。
　　　　　これがそのまま a^n－r b^r の係数 になる。
 　　すなわち、上右の _○C_○ の図が元々のパスカルの三角形である。

２．上右図の左端は一般化すると _nC₀ だが、_nC₀＝1 である。
 　　※　「n 個の中から 0 個取る」 場合の数は 「何も取らない」 という１通り。
　　また、上右図の右端は一般化すると _nC_n だが、_nC_n＝1 である。
 　　※　「n 個の中から n 個取る」 場合の数は 「全部取る」 という１通り。
　　→ 以上から 「パスカルの三角形の両端の数は 1 」 であることが確認できた。

３．パスカルの三角形は左右対称である。そのことを式で表すと _nC_r ＝ _nC_n－r となる。
 　　※　「40人のクラスで運動会の棒倒しに出場する38人を選ぶ」には「出場しない2人を選ん」でも同じこと。
　　　　　すなわち ₄₀C₃₈ ＝ ₄₀C₂ 。一般に _nC_r ＝ _nC_n－r が成り立つ。

４．パスカルの三角形で 「上段の２数の和を、２数の真ん中下段に書く」 とした部分は、
 　　一般的には _nC_r ＝ _n－1C_r－1 ＋ _n－1C_r という式で書ける。
 　　※　「40人のクラスで10人の掃除当番を選ぶ」 場面を想定してみよう。
　　　僕自身は選ばれたくないが、選ばれてしまうかもしれない。
　　　僕自身が選ばれない（ラッキーな）場合は、僕以外の39人の中から10人選べば良いので ₃₉C₁₀ 通り。
　　　僕自身が選ばれる（アンラッキーな）場合は、僕以外の39人の中から9人選べば良いので ₃₉C₉ 通り。
　　　その両方を合わせたものが総数 ₄₀C₁₀ だ。
　　　すなわち ₄₀C₁₀ ＝ ₃₉C₉ ＋ ₃₉C₁₀ 。一般に _nC_r ＝ _n－1C_r－1 ＋ _n－1C_r が成り立つ。

　以上から、先ほど書いた単純な操作の繰り返しで (a＋b)ⁿ の展開式の各項の係数を書き出せることが示せた。めでたし、めでたし。

なぜ小学校でプログラミング教育が要るのか？

　「小学校にプログラミング教育を導入」という話がある。そうすると多くの人はまず「そもそも小学生にプログラミングが必要なのか？」と考える。いま現在無いものだから、新たにそれが入るという話になると、現状を「変えるのか？　変えないのか？」と反応するわけだ。
　けれども、それでは前に進まない。「要るか、要らないか」を考えることは無駄とは言わないまでも、もともと私たちの脳の習慣として「現状維持バイアス」があるようで、そうであれば意識して「なぜ要るのか？」と考える方がそのバイアスを軽減する意味でも効果的だと思うのである。

　というわけで、小学校でプログラミング教育が「要るのか？　要らないのか？」を考えることはせずに、要るという前提に立って「なぜ要るのか？」を考えてみた。

---

◇　プログラミングとは「数学的な考え方をもとに物理的にものを動かす」こと。
　　部分的に動かす（プログラミング）ことだけでなく、全体の中での位置づけも認識させたい。

◇　人間の役割は「アルゴリズムを作る」こと、それに従って処理するのがコンピュータ、ＡＩ（人工知能）も同じ。
　　その際に指示を「コンピュータに理解できる言葉」で語るのがプログラミング。

◇　プログラミングを「コンピュータとのコミュニケーション」と考えれば「人とのコミュニケーション」にも役立つ。
　　どのように伝えれば相手は動いてくれるのか、相手は何を欲しがっているのか、自分は何がしたいのか。

◇　抽象化思考（具体的なものを抽象化して考える力）を身につける方法として、プログラミングがちょうどいい。
　　プログラミングを通して算数・数学の一部を学習するとより効果的。

◇　「小中学校教育の入口にプログラミングがある」という考え方も良い。
　　たとえば命令のコマンドは英語に、画面上の点の位置は数学の座標に通じる。

◇　今どき何か新しいことをやろうと思ったら、ほとんどの場合コンピュータやインターネットが絡むはず。
　　「コンピュータで何ができるのか、どれくらいの作業量でできるのか」が見積れなかったら仕事に関われない。

◇　ＡＩ（人工知能）が人間から仕事を奪うというけれど、むしろＡＩは人間にたくさんの新しい仕事を与えてくれる。
　　コンピュータと「競争」するのではなく、コンピュータと「共生」すると考えよう。

---

がぁーっと書いてみた。

エクセルはどこまで正確に計算できるか？

　手元にある電卓で「1÷3×3＝」と入力すると、「0.9999999」という結果になった。「1÷3」は割り切れないので、電卓の中では計算結果が「0.3333333」となって、それを3倍して「0.9999999」になったというわけだ。
　ところで、同じ電卓で「1×3÷3＝」と入力したら、結果は「1」になった。電卓は入力した順番に計算すると考えれば、そうなることはなるほど納得できる。

　さて、エクセルはどこまで正確に計算できるのだろう？

(1)　セルA1に「=1/3」を入力して、小数点以下の表示ケタ数を増やしてみた。
　　小数第何位まで正しく表示するだろうか？　（※1 をクリック）

(2)　セルB1に「=1/2」を入力して、セルB2に「=B1/2」を入力して、
　　セルB2の式を下方向にコピーした。何行目まで正しく表示するだろうか？

(3)　セルC1に「=2」を入力して、セルC2に「=C1＊2」を入力して、
　　セルC2の式を下方向にコピーした。何行目まで正しく表示するだろうか？
　（ただし、(3)のC列では ※2 の▼印をクリックして、「数値」を選ぶ）

その結果・・・
(1)　小数点以下20位まで表示してみたところ、「3」が15個並んで、それ以降は0となった。
　　これは小数第16位を四捨五入して、小数点以下15位までで表した値と一致する。

(2)　21行目までは正しく表示したが、22行目で値が合わなくなった。
　　21行目（1/2²¹ の値）は 0 でない数が小数第7位から小数第21位まで続く数であるが、
　　つまり15ケタ分は正しく表示したことになる。
　　22行目（1/2²² の値）は 0 でない数が16個続く数になるが、15個までは正しく表示して、
　　16個目の数字が 0 になってしまっている。

(3)　49行目までは正しく表示したが、50行目で値が合わなくなった。
　　49行目（2⁴⁹ の値）は15ケタの整数で正しく計算したが、
　　50行目（2⁵⁰ の値）は16ケタ目が 0 になってしまっている。

　以上 (1),(2),(3) からわかること。それは、エクセルは有効数字にして15ケタ程度までは正しく計算できるが、それ以上になると正しく計算できなくなるということだ。
　15ケタというと、整数値の場合、数百兆のレベルになる。それを超えた数、つまり一千兆のレベルはエクセルで正確には計算できないことになる。では、エクセルでは一千兆を超えた数は扱えないのかというと、そういうことではない。それについては、また 次回 。

１　→　２　→　３　→　４　→　５　→　６

エクセルはどこまで大きな数、細かい数を扱えるか？

(1)　セルA1の値を 10 として、セルA2の式を「= A1＊10」として、その式を下方向にコピーする。
(2)　セルB1の値を 0.1 として、セルB2の式を「= B1/10」として、その式を下方向にコピーする。
（ただし、セルの表示形式は「標準」のままとする）

ところでこの場合、値が大きくなると、あるいは 0 に近い値になると、指数形式で表示される。たとえば、セルA11の「1E+11」は「1×10¹¹」を表し、セルB10の「1E-10」は「1×10⁻¹⁰」を表す。

　さて、下方向にコピーしたとき、どこまで大きな数、細かい数を表せるか？
　A 列では 1×10³⁰⁸ までは表示できたが、それより大きくなると「エラー」表示が出た。B 列では 1×10⁻³⁰⁷ までは表示できたが、それより細かい値になると「0」と表示された。
　ところで、これは「整数値は 308 ケタまで、小数は小数点以下 307 位まで『正確に』計算できる」ということではない。エクセル内部では値を

a ×10^b　（ただし、1 ≦ a＜10 , b は整数）

の形で表現しているが、仮数部 a と指数部 b の精度が異なるからである。いうなれば、値の正確さは a で、値の大きさは b で決まる。上の例は、正確さを調べたのではなくて、扱える数の大きさを調べたのである。前の記事 で示したように、仮数部 a が正確に計算できるのは 15 ケタ程度である。すなわちエクセルでは、必ずしも正確とは限らないが、「およそ 10⁻³⁰⁷ から 10³⁰⁸ 程度までの計算を扱える」ということである。

１　→　２　→　３　→　４　→　５　→　６

浮動小数点形式はエクセルでこそ力を発揮する

　浮動小数点形式の数は「a×10^b」と表す。たとえば、10進数の 123 を浮動小数点形式で表すと 1.23×10² となる。また、２進数も浮動小数点形式で表すことができる。10進数の 123 を２進数で表すと 1111011 となるが、これを２進数の浮動小数点形式にすると 1.111011×10¹¹⁰ となる。なお、この場合は、指数の部分も２進数表示したものだから、「×10¹¹⁰」はつまり「×2⁶」のことである。
　a を仮数部といい、b を指数部という。要するに、仮数部 a が数字の並びを表し、指数部 b が位取りを表すということだ。a が数の精度を表し、b が大きさを表すといってもよい。
　さて、コンピュータ内部では２進数で処理しているが、エクセルでは数を仮数部と指数部に分けて認識している。具体的には、仮数部に（符号も含めて）52ビット、指数部に（符号も含めて）12ビットを割り当て、合わせて64ビット（＝8バイト）を使って１つの数を表現している（「倍精度」の場合）。

1.0101…0101×10^101…010
  └　仮数部　┘　└指数部┘
　　52ビット　　　12ビット

※ 仮数部の先頭（整数部分）は必ず 1 なので、無視する。

　仮数部に52ビット割り当てた結果として10進数で15ケタまで正確に計算できる（→詳細は こちら）ことになる。また、指数部に12ビット割り当てた結果として10進数で 10³⁰⁰ のような大きな数や 10⁻³⁰⁰ のような細かい数も扱える（→詳細は こちら）ことになるというわけだ。

１　→　２　→　３　→　４　→　５　→　６

エクセルに計算ミスさせろ

　エクセルで 1/3 を足し続けたらどうなるか？
　手順は、セルA1に「=1/3」を、セルA2に「=A1+1/3」を入力し、セルA2の式を下方向にコピーする。こうすれば、計算上は n 行目のセルAnで n/3 の値を表示することになるはずである。
　1/3は割り切れない（循環小数）が、セルA1では四捨五入して小数第15位までの数が正しく表示されている。前の記事に書いたとおりである。セルA2でも同様に、四捨五入して小数第15位までの数が正しく表示されている。セルA3は「1/3+1/3+1/3」となるが、表示は「1」と正しく表示された。
　さて、さらに下方向にコピーを続けても、正しく計算するだろうか？
　次に、数値を変えてやってみよう。1/3 を 0.1（=1/10）に変えたらどうなるか？また、0.5（=1/2）に変えたらどうなるか？誤差が生じるだろうか、それとも誤差が生じないだろうか？

　上表を見ての通り、1/3 と 0.1 の場合は誤差が生じたが、0.5の場合は誤差が生じなかった。
　ところで、足し続ける数値によって、あるときは誤差が生じ、あるときは誤差が生じないのはなぜなのか？　それについては、また あと で。

１　→　２　→　３　→　４　→　５　→　６

エクセルはとことん２進法で計算する

　前の記事「エクセルには誤差がある」で、エクセルで「0.5を足し続けても誤差を生じないが、1/3 や 0.1 を足し続けると誤差が生じる」ことを示した。さて、その訳は、何なのだろう？
　それは、10進数の 0.5 , 1/3 , 0.1 を２進数で表してみるとわかる。エクセルでは10進数を入力して、計算結果を10進数で表示するが、計算そのものは２進数で実行しているからである。
　まず、0.5 から。10進数の 0.5 を２進数で表すと 0.1 となる「0.5₍₁₀₎＝1/2₍₁₀₎＝1/10₍₂₎＝0.1₍₂₎」。つまり、２進数で表したとき、これは「割り切れる数（有限小数）」だ。
　次に10進数の 1/3 を２進数にしてみよう。そのために、まず分母の3を２進数にしてみると 11 となる。つまり、1/3₍₁₀₎＝1/11₍₂₎ である。そこで、実際に割り算してみよう。もちろん、２進数の割り算をするのだが、10進数の割り算と若干異なるけれども、手順はほとんど同じである。
　同じように、10進数の 0.1 を２進数にしてみよう。0.1₍₁₀₎＝1/10₍₁₀₎ で、分母の 10 は２進数で 1010_(２)だから、２進数の割り算 1÷1010 を実行すればよい。
　その結果は、次の通りである。

　10進数の 1/3 は割り切れない数（循環小数 0.3333…）だが、２進数でも割り切れなかった（循環小数 0.0101…）。10進数の 1/10 は割り切れる数（有限小数 0.1）だが、２進数では 0.000110011… とこれも循環小数になった。だから、コンピュータの中では 1/3 や 0.1 を正確に計算することはできないのである。コンピュータは有限個のものしか扱えないので、無限小数はどこかの位で丸めて処理することになって、だから誤差が発生するのである。
　ちなみに、現行の学習指導要領では、上のような２進数の割り算や循環小数についても高校・数学で扱う。というわけで、この記事は高校・数学科と高校・情報科のコラボ・ネタである。

１　→　２　→　３　→　４　→　５　→　６

練習問題（エクセルの限界に挑む）

(1)　2進数の整数 101010 を10進数で表すと（ ① ）であり、2進数の小数 0.101 を10進数で表すと（ ② ）である。また、16進数の２桁の整数 AB を10進数で表すと（ ③ ）である。

(2)　エクセルで 1/3 を足し続けたらどうなるかを実際に試してみた。まず A 列に上から順に 0,1,2,3,… と入力した。また B 列と C 列を小数点以下20桁まで表示するようにした。
　次にセル B1 に 0 を入力し、そこに 1/3 を足した値をセル B2 として、その式を下方向にコピーしたところ、下表のようになった。

	A	B	C	D
1	0	0.00000000000000000000	0.00000000000000000000
2	1	0.33333333333333300000	0.33333333333333300000
3	2	0.66666666666666700000	0.66666666666666700000
4	3	1.00000000000000000000	1.00000000000000000000
：	：	：	：
21	20	6.66666666666666000000	6.66666666666667000000	×
：	：	：	：
128	127	42.33333333333340000000	42.33333333333330000000	×
：	：	：	：
142	141	47.00000000000010000000	47.00000000000000000000	×
：	：	：	：

ところで、10進数の 1/3 を小数に直すと、右の計算により循環小数になる。これを「0.3」と表す。上表のセル B1 ～ B2 をみると、途中で四捨五入されているが、小数点以下15桁くらいまで正確に表示されていることがわかる。
　さて、その関数式をさらに下方向にコピーしてみたところ、何か所かで計算が合わないところが見つかった。ところで、計算が合わないところを目で探すのは意外と難しい。そこで、エクセル自身にそれを発見させるようにしよう。そのために、まず A 列の各セルに 1/3 を掛けた値を C 列の同じ行に表示させることにした。これが四捨五入したときの正しい値で、いわば理論値にあたる。その上で、IF 関数を使って、B 列と C 列の値が異なれば D 列に 「×」 を表示させ、同じ値なら D 列に何も表示させないようにした。こうすればどこで誤差を生じたのかが一目でわかる。
　ところで、なぜ誤差が生じるのだろう。それは10進数の1/3を2進数の小数で表してみるとわかる。エクセルでは10進数を入力して、計算結果を10進数で表示するが、計算そのものは2進数で実行しているからである。

①　上表のセル B2 , C1 , D1 に入る関数式を書きなさい。
　　ただし、下方向にコピーして正しく動く式を答えること。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
②　10進数の 1/3 を2進数の小数で表しなさい。
　　ただし、 循環小数になる場合は「0.1001」のように表すこと。

---

《解答》
(1)　①　42　　②　0.625　　③　171
(2)　①　B2　　＝ B1＋1/3
　　　　 C1　　＝ A1＊1/3
　　　　 D1　　＝ IF (A1＝B1 , "" , "×")
　　 ②　　　　 0.01

１　→　２　→　３　→　４　→　５　→　６

数学嫌いは「好き」の裏返し

○ 「数学が嫌い」は「好き」の裏返し。数学のことがとても「気になっている」ことの証し。

○ 「数学が苦手」は「得意になりたい」という期待の現れ。きっかけをつかもうとしている。

○ 「数学なんか役に立たない」は「役立てたい」という願い。数学が使える場面を探っている。

---

　「好き」の反対は「嫌い」じゃありません。「好き」の反対は「無関心」。関心がなければ、好きにも嫌いにもなりませんね。関心があってこそ好きになったり嫌いになったりするわけで、つまり「好き」と「嫌い」は実はすごく近いのです。どちらも「気になっている」という意味では、同じカテゴリーにあるのです。
　たとえば「歴史が嫌い」という人はあまりいません。「歴史に興味がない」という人はいるでしょうけれど、彼らは「歴史が嫌い」とは言いません。好きとか嫌いとか言う以前に「興味がない」のであれば、好きにも嫌いにもならないわけです。
　同じように「家庭科が苦手」という人もあまりいないでしょう。「上手になりたい」という気持ちがなければ、苦手だという意識は出て来ませんから。
　「理科なんか役に立たない」という声もあまり聞きませんね。化学でも物理でも生物でも、そんなもの知らなくても生活する上で困らないといえば困らないわけです。その意味では数学も理科も同じなのですが、数学に限って「役に立たない」と言う人が多い。その差は、どこかで「役立てたい」という思いがあるか無いかの差なのではないでしょうか。

　実はみんな「数学が好きに、得意になりたい。いろんな場面で数学を使いたい」と思っているのです。そうでなければ、他の教科ではあまり聞かない言葉、すなわち「嫌い、苦手、役に立たない」が数学で際立って言われるはずがないのです。


※　僕は受験数学は嫌いです。苦手です。あんなもの本当に役に立たないと思っています。

猿と人の違い

　「植物と動物の違いは？」と聞くと、知識の問題になる。「哺乳類と鳥類の違いは？」と聞いても、やっぱり知識の問題になる。学校で習うことだから。そしてそこには正解と間違いがある。つまり○か×がつく。こうなると面白くない。
　でも「猿と人の違いは？」と聞くと、様相が変わる。知識では答えられないからだ。いろんな答え方がありそうで、単なる○か×かではない、まったく別の問いに変わる。それに答えるためには、いやでも想像力を働かせることになる。生物学的視点からの答え方もあるだろうし、社会学的視点からの答え方もあるだろう。動物園の猿を見物する自分という人の視点などなど、想像力はいくらでも広がる。

　前者の問いは、単なるクイズだ。それに答えられても、将来役にたつかどうかは分からない。それに答えられなくても、将来役にたつ人にならないとも限らない。
　むしろ後者の問いの方が、将来役にたつんじゃなかろうか。その問いに黙ってしまう人より、がんばって何とか答えようとする人の方が将来使えるんじゃなかろうか。

　ここで、ちょっと考えてみませんか。「猿と人の違いは何だろう？」。とりあえず３つくらい挙げてみてください。
　と、ここまで書いてきて気づきました。前者と後者の問いの違いは何か？
　前者の問いに答える際には、考えない。後者の問いに答えるには、考える。違いは、これじゃなかろうか。たったこれだけの違い。けれども、決定的な違い。

隠すことと晒すこと

人と他の動物の違いはなんだ？

	ヒト	動物
食事	晒す	隠す
排泄	隠す	晒す
交尾	隠す	晒す

いろんな点で真逆ですね。

カーリングのストーンはなぜ滑るのか？

　カーリングのストーンはなぜ滑るのだろう？
　固体どうしが接触する場合、基本的には滑らない。たとえば、平らな土の上にある石は滑らない。ところが、カーリングのストーンは固体である氷の上を滑る。なぜなのか？
　答は、固体の氷が溶けて、液体の水になるからだ。では、なぜ氷が溶けるのだろう？
　ストーンが動くことによって発生する摩擦熱？　もしそうだとすると、カーリングの会場はすぐに水浸しになるだろう。なにしろ１試合で10エンド、１エンドあたり各チーム10回ずつストーンを投げるのだから、１試合で合計200回もストーンを投げるのだ。その度に氷が溶けたら、試合が終わる頃にはカーリング会場は水浸しになって、氷がすっかり無くなってしまいそうだ。

　なぜそうならないのか？　その訳は、溶けて水になった氷がまたすぐに凍るからだ。でも、冷えて凍るわけじゃない。
　ではそろそろ、そのカラクリを説明しよう。氷はストーンの圧力が加わることによって溶けるのである（右図の赤線）。そしてストーンが通り過ぎると圧力が下がって再び凍る（右図の緑線）。つまり氷はストーンが通り過ぎるその瞬間だけ溶けて、すぐに元に戻る。こうしてストーンが氷の上を滑りながら移動するわけだ。温度変化（グラフの左右への移動）ではなくて、圧力の変化（グラフの上下移動）によって「固体→液体→固体」と変わるというわけである。
　スキーもスケートも、また雪道で滑って転ぶのも同じ理由による。

数学的正しさで物事を解決しようとする人とは、なぜ議論が成り立たないのか？

　数学的な正しさは、条件を厳密に設定して、その中でのみ成り立つ正しさです。そこでは「100％絶対に正しい」ものだけを「真」といい、反例が１つでもあったら「偽」とします。「99％正しい」ものも「まるでデタラメ」なものもひっくるめて「偽」です。
　ところで、日常の議論においては「誰が見ても絶対に100％正しい」ようなものは、最初から議論の対象になりません。人によって見方・考え方が違うから議論になるのです。そしてそこで目指すものは「意思決定」です。それが「絶対に正しいものではない」ことを承知の上で、より良い選択をしようとするわけです。

　言い換えると、数学の論理は「そぎ落とす」論理です。あいまいさ（境界）をそぎ落とし、ニュアンス（豊かさ）をそぎ落とし、背景（個別事情）をそぎ落として、骨格だけを抜き出して、真偽判定に持ち込みます。
　一方、議論の論理は「取り込む」論理です。いろんな見方・考え方を取り込み、異論・反論までも取り込みます。そして、それらすべてを勘案して「意思決定」しようとします。
　すなわち「数学的正しさ」で物事を解決しようとする人は「視野を狭める」ことでそれを為そうとするのに対して、「意見を出し合って」物事を解決しようとする人は「視界を広げる」ことでそれを為そうとするわけです。

　数学的正しさで物事を解決しようとする人にしてみれば、相手の言い分は「前提を覆してばかり」で、単なる「言いがかり」のように見えるでしょう。一方、意見を出し合って物事を解決しようとする人からみれば、相手はまるで「人の話を聞こうとしない、議論する気がない」ように見えるでしょう。
　だから両者の間では議論が成り立たないのです。目指すべき目標（真偽判定か意思決定か）も違えば、そこに向かうための道筋（視野を狭めるか広げるか）も違うのですから、かみ合うはずがないのです。

無限ってなんだかいかがわしい

　前に出した問題「板をズラして積み上げる」の続きです。

---

【問】大きさ・重さが同じ板が４つある。
　　　１つの板の長さを１とする。
　　　これらを右のように積み上げる。

　(1)　全体の長さ（全長）は、どこまで長くなるかな？

　(2)　板がもっとたくさんあったら、どうだろ？
　　　無限個積み上げたら、どこまで長くなるんだろ？

　崩れちゃダメだよ。

---

　この問題の (2) の《答え》は「板を無限個積み上げたら、全長は無限に長くなる」でした。
　ここではもう少し具体的に「板をどの高さまで積み上げたら、全長はどれくらい長くなるか？」を見ていこう。
　まず、板の長さを 10cm、厚さを 1cm とする。どこにでもありそうな板だろう。その板の枚数をどんどん増やしていって、高く高く積み上げて、板がどこまで横に長くなるかを調べてみた。

　板の枚数が５枚までは正確に計算した。５枚積んだ時点で、板の長さの２倍の 20cm を超えた。
　それ以上まともに計算するのは無茶なので、先ほど示した式

1＋1/2＋1/3＋ … ＋1/n ＜ 1＋log n

の右辺 1＋log n を使って、n 枚積み上げたときの板の全長 L を求めてみた。不等号の向きから分かるように、それは若干多めに見積もった長さである。理論的な全長 L はそれよりいくらか短い値になる。
　10 枚積み上げると 26cm、100 枚積み上げる（高さ 1m）と 38cm 。思ったほど長さが伸びない。そこで一気に東京スカイツリーの高さ（648m＝64,800枚）まで積み上げると 70cm、エベレスト山の高さ（8,848m＝884,800枚）まで積み上げても 83cm 。全長 L はまだ 1m に届かない。
　ヤケクソというわけではないが、月まで積み上げたら、さすがに 1m を超えた。太陽まで積み上げたら、さらに伸びたものの、2m には届かない。

　そう、「全長 L が無限に長くなる」と言っても、その増え方はこんなものなのである。理屈では無限大であっても、現実には 1m にも達しないのだ。無限ってなんだかいかがわしい。こんな事例 もあった。

無限のいかがわしさ

農地的な生き方

自然と都会の間に農地がある。
農地は自然そのものではない。そこには人の手がたくさん入っている。
農地は完全な人工物でもない。自然の力がなければ、農地は成り立たない。

手つかずの自然の中では、暑ければ耐え、寒くても耐える。
都会では暑ければ冷房して、寒ければ暖房して、いつでも手ごろな温度になるように操作する。
農地では気温の変化を頼りにして、適宜人の手を加えながら、季節に応じて作物を育てる。

手つかずの自然の中で雨が降ったら、流れるも溜まるも自然任せで、元に戻るには時を待つしかない。
都会では遠い場所から水を引く一方で、都会に降った雨は一刻も早く海へ流そうとする。
農地では降った雨をなるべく有効に利用することを考える。

手つかずの自然の中では蛇に噛まれたら諦めるしかない。責任はどこにも誰にも無い。
都会ではレストランで食べて腹をこわしたり、学校で子供が怪我したりしたら訴えればいい。責任は他者にある。
農地ではなるべく不具合が起きないように手を施すが、なかなか思い通りにはならない。責任は自分で負う。

手つかずの自然の中ではお金は全く何の役にも立たない。頼れるのは自分だけだ。
都会ではお金がすべてである。お金が無ければ何もできない。お金があれば何でもできる。
農地では自分に必要な物のうちのある程度は自分の土地で賄って、お金を介して他の物を手に入れる。

私は手つかずの自然に憧れているわけでもないし、都会暮らしに疲れたというつもりもない。
人間はクマやカエルやコオロギのように暮らしてはいけないし、また機械になることもできない。
人間は自然そのものではないし、もちろん人工物でもない。その中間、いわば農地のような存在だと思うのだ。

人間の体は農地だ。自然には逆らえないが、調子が悪ければ手を入れて整えたいと思う。
脳ミソも農地だ。適当に耕したり休ませたりしながら、力を発揮できるような土壌を作りたい。
子供も農地だ。計画通りに育つはずもないので、各自の中に宿る自然の力を引き出すべく手を入れる。

幸いなことに、私の実家には狭いながらも農地があって、両親が田んぼで米を作り、畑で野菜を作っている。
今は２人とも元気だが、けっこうな年だから、このままではやがて耕作放棄地になるかもしれない。
私は子供の頃は多少は手伝いもさせられたが、今は都会に住んでいて農業はまったくやっていない。
ちょうどいい頃合いだ。そろそろ農業をやりながら、農地的な生き方をしてみるのも悪くなさそうだ。

自然は、人の都合などお構いなしに好き勝手に振る舞って、しばしば人に危害を加える。
都会は、自然が人間になるべく影響を与えないように、その力をできるだけ無力化しようとする。
農地は、自然の力をあてにして、手を入れながら、自然の力を引き出そうとする。

世界一簡単な言語は楽譜である

　楽譜に載っている情報は、音の高さと長さだけ。これってつまり、世界一簡単な言語ってことなんじゃないだろうか。
　日本語と比べてみよう。日本語にはひらがな・カタカナ・漢字を合わせれば文字の数が何千もある。文字を組み合わせて意味を成し、異なる意味を持つたくさんの単語がある。また、それぞれの文字に音があり、同じ文字でも読み方が違ったり、違う文字なのに読みが同じだったりして複雑極まりない。
　英語のアルファベットの数は日本語ほど多くないが、それでも楽譜の中の音の高さと長さの種類よりはだいぶ多い。そしてアルファベットを組み合わせることで膨大な種類の意味を持たせるという点において、英語の複雑さは楽譜とは比べ物にならない。
　言語としてもう１つ挙げるなら、プログラム言語。これもアルファベットの組み合わせでプログラムのコードを書くのだが、命令の種類、文法の種類はやっぱり楽譜の中の音の高さと長さの種類よりはるかに多い。しかもプログラム言語は条件で分岐したり、ループして繰り返したりする。音の長さに従ってただ一方向に進む楽譜と比べて、やっぱりプログラム言語ははるかに複雑である。
　楽譜は音楽の言語である。音の高さ・長さ以外に音の強弱やリズムもあると言えば言えなくもないが、それを言うなら日本語や英語にだって声のトーンや声色みたいなものがあるのだから、結局のところ楽譜という言語が日本語や英語よりずっと簡単であることに変わりはない。
　ちなみに、それほどまでに簡単な楽譜を僕は読めないのだが、そんなことは今の話題に直接関係ないので深く立ち入らないことにして、いずれにせよ「楽譜が世界一簡単な言語である」ということは揺るがないのと思うのだが、いかがだろうか。

★ そもそも議論とは何なのか？

〜 屁理屈から理屈を取ったら屁だけが残る 〜

☆　論理式はデジタル仕様
（→ https://omori55.blogspot.com/2019/03/blog-post_21.html ）

　　◇　１枚のカード問題
　　◇　４枚のカード問題
　　◇　天秤ばかりのおもりはなぜ２進法なのか？


☆　説明しない人々
（→ https://omori55.blogspot.com/2019/03/blog-post_957.html ）

　　◇　レストランのおすすめメニュー
　　◇　おまわりさんと三文判
　　◇　身元引受人はつまり何を引き受けるのか？


☆　阿吽（あうん）の呼吸の作り方
（→ https://omori55.blogspot.com/2019/04/blog-post_396.html ）

◇　相手の立場でものを言う
◇　相手の気持ちを慮る
◇　わかり合う

☆ 正しい議論は無意味である

　絶対に正しい議論とは、実は無意味な議論なのです。３例示します。

　　◇　カラスは黒いのか？　
　　◇　「ソクラテスは死ぬ」のか？　
　　◇　バカを論証する　

　日常の論理に「反例があるから偽」というルールを適用したら、大抵のことは偽になってしまいます。日常の論理に絶対の正しさを求めたら、ほとんど無意味な発言しかできません。

カラスは黒いのか？　　「ソクラテスは死ぬ」のか？　　バカを論証する

カラスは黒いのか？

　命題「素数は奇数である」は偽です。反例があるからです。「2」は素数ですが、奇数ではありません。
　命題「4の倍数は偶数である」は真です。これは証明できます。そして、反例はありません。論理的には、

◇　真であることを示すには証明する
◇　偽であることを示すには反例をあげる

そうすることで、真偽がはっきりします。
　ところで、このルールを日常の論理に適用すると、大抵のことは偽になってしまいます。

　さて、カラスは黒いのでしょうか？
　これが真だと証明できるかというと、すべてのカラスをチェックすることは現実的には無理ですね。ということは、真であることを示せないということです。
　それでもガンバってチェックしてみるとどうなるでしょうか。おそらく、やがて反例に巡り合って、「カラスは黒い」が偽であることを示す結果になるでしょう。突然変異で黒くないカラスだってどこかにいるでしょうから。
　「Ａさんは正直者である」という文も、「正直者＝ウソをついたことが無い」と解釈すると、偽になるでしょう。誰だって一度くらいはウソをついたことがあるでしょうから。
　だからといって、「誰でも一度はウソをついたことがある」と言ったら、これもたぶん偽になります。世界中に一人くらいはウソをついたことがない人だっているでしょうから。
　少なくとも、どちらの文も真であると証明することは不可能です。

　さて、カラスの話に戻りましょう。ではどうすれば、カラスの色について論理的に正しい表現ができるでしょうか。
　「カラスは黒い。ただし、例外を除く」はどうでしょうか。いいえ、こんなのは全然ダメです。これが良いなら、「地球は平らである。ただし、例外を除く」も良くなってしまいます。
　「大抵のカラスは黒い」はどうでしょうか。いいえ、これも全然ダメです。まず「大抵」というのがあいまいですし、そもそも統計を取らずにそんなことが言えるはずがありません。
　「私が見たカラスは黒かった」というのはどうでしょうか。残念でした、これもダメです。これは「私が見た宇宙人には目が３つあった」というのと同じで、「勝手に言ってろ」という話です。

　カラスの色について論理的に正しい表現は１つしかありません。それは「黒いカラスは黒い」です。
　日常の論理に「反例があるから偽」というルールを適用したら、大抵のことは偽になってしまいます。
　日常の論理に論理学的な正しさを求めたら、ほとんど無意味な発言しかできません。

カラスは黒いのか？　　「ソクラテスは死ぬ」のか？　　バカを論証する

「ソクラテスは死ぬ」のか？

　論理学の教科書にしばしば出てくる例に、次のようなものがある。

前提１：すべての人間は死ぬ（べき存在である）。
前提２：ソクラテスは人間である。
結論：よって、ソクラテスは死ぬ（べき存在である）。

前提１と前提２から結論が導けるから、これは正しい演繹である。

　ところで、これは「ソクラテスは死ぬ（べき存在である）」ことを証明したことにはならない。
　なぜか？　結論が正しいと言えるためには前提１と前提２が正しくなければならないのだが、前提１と前提２を吟味してみると、それらが正しいかどうだか怪しいのである。
　まず、前提１について。これまでに死んだ人を書き連ねても、前提１が正しいことを示したことにはならない。前提１が正しいことを示すためには、いま生きている人とこれから産まれてくる人がすべて死ぬことを示さなければならないが、それは不可能だ（まぁ人類が滅亡すると言えればいいんだが、それは予言であって、証明ではない）。つまり、前提１が正しいことはどう転んでも示せないのである。だから、結論が正しいとは言えないのである。
　前提２「ソクラテスは人間である」を正しいものとして前提１を考えると、またまたおかしなことが起きてくる。「すべての人間」の中には当然ソクラテスも含まれる。だから「ソクラテスが死ぬ」ことを確認してからでないと、「すべての人間が死ぬ」ことが言えないのである。結論が成り立たなければ、前提１は成り立たないのである。つまりこの論法は、結論を認めた上で、いったん前提１へ迂回して、再び結論が成り立つと主張しているのだ。
　次に、前提２について。これを示すためには、まず「人間」を定義しなければならない。「条件・・・を満たすものを人間という」と。その上で「ソクラテスは・・・を満たすから、ソクラテスは人間である」と、このように前提２を示すことになる。
　しかしこれも単に迂回しているにすぎない。なにもソクラテスを含む集団を定義しなくても、ソクラテスだけを定義すれば十分である。そうすると、前提２は「前提」というより、「定義」そのものになる。つまり、前提２は「ソクラテスを人間と定義する」というのと実質的に同じである。要するに、前提２は「正しいか正しくないか」という問題ではなくて、単に一方的に「宣言」しているにすぎない。

　以上をまとめると、上の論は、

定義：ソクラテスを人間とする。
前提：ソクラテスを含むすべての人間は死ぬ。
結論：よって、ソクラテスは死ぬ。

と同じである。そしてこの論は、「人間」に言及しなければ、

前提：ソクラテスと他のある者は死ぬ。
結論：よって、ソクラテスは死ぬ。

と同じである。さらに、「他の者」に言及しなければ、

前提：ソクラテスは死ぬ。
結論：よって、ソクラテスは死ぬ。

と同じである。

　演繹とはそういうものだ。前提から結論を導くことはできても、結論が正しいことは示せない。前提が正しいことを示せないからである。前提が結論を含んでいるから、必然的にそういうことになる。

カラスは黒いのか？　　「ソクラテスは死ぬ」のか？　　バカを論証する

バカを論証する

　次の２つの文のうち、絶対に正しいのはどちらでしょうか？

（文１）～～と言う人はバカである。○○は～～と言った。よって、○○はバカである。
（文２）○○は～～と言った。よって、○○はバカである。

（文１）を「命題」と受け取れば、これは絶対に正しい。誰が見ても正しいはずです。典型的な３段論法です。一方、（文２）は絶対に正しいとは言えない。誰が見ても正しいとはとても言えないでしょう。
　ところで、（文１）と（文２）を比べてみると、（文２）は（文１）の一部です。（文２）に「～～と言う人はバカである」という条件を付け足したものが（文１）です。つまり、（文２）だけでは正しくないけれど、それにもう１つの条件を付け足すことで、（文１）が正しい文になるということです。
　でも、（文１）の方が（文２）よりも優れていると考えたら、大間違いです。（文２）は（文１）の出来そこないだと考えるのも、大間違いです。説明しましょう。

　「（文１）が正しい」という意味は、「前提から結論を正しく導いている」という意味です。決して、「前提が正しい」ということでもないし、「結論が正しい」ということでもありません。つまり、（文１）は絶対に正しいのだけれども、「○○がバカである」ことを示したことにならないのです。
　（文１）において「結論が正しい」ことを言うためには、「前提が正しい」ことを言わなければなりません。さて、どうやったら「前提が正しい」ことが言えるでしょうか？
　ここで２つ目の前提「○○は～～と言った」は正しいものとしましょう（現実には「誤解だ、曲解だ、揚げ足取りだ」のように、ここが問題になることが多いのですが、ここではそういうことは除外して考えます）。そうすると、１つ目の前提「～～と言う人はバカである」が正しければ、結論が正しいことになります。
　では、どうすれば「～～と言う人はバカである」が正しいことを示せるでしょうか？　ここでちょっと、それと（文２）を見比べてください。

（文１）’～～と言う人はバカである。（文１の前提）
（文２）○○は～～と言った。よって、○○はバカである。

（文１）’は（文２）よりはるかに多くのことを述べなければならないことがお分かりいただけるでしょうか。（文２）は「○○は～～と言ったから、○○はバカだ」と言っているのに対して、（文１）’は「～～と言う人は、みんなバカだ」と言わなければならないのです。（文２）は「特定の場面において、特定個人のことだけ」を言えばいいのに対して、（文１）’では「誰であっても、どんな場面であってもそれが成り立つ」と言わなければならないのです。（文１）’が正しいと示すことは、（文２）が正しいことを示すより、ずっとハードルが高いのです。当たり前です。（文１）’は（文２）を含んでいるからです。
　ところで、（文１）も（文２）も結論は同じです。「○○はバカである」、これがゴールです。では、スタートは？というと、（文２）にとっては「○○は～～と言った」こと、これがスタート（根拠）です。
　では、（文１）にとってのスタートは何でしょう？　形式的には「前提」が（文１）のスタートなのですが、先ほども申しあげたように、それでは結論が正しいことを示したことにならないのです。それでは、ゴールにたどり着かないのです。「○○はバカである」というゴール（結論）にたどり着くためには、上記（文１）’を示さなければならなくて、それは（文２）を含みますから、結局のところ（文１）のスタートラインは（文２）のそれと同じだと考えざるをえないのです。
　ここでもう一度（文１）と（文２）を見てみましょう。

（文１）～～と言う人はバカである。○○は～～と言った。よって、○○はバカである。
（文２）○○は～～と言った。よって、○○はバカである。

（文１）は絶対に正しくて、（文２）は正しいとは言えないわけです。（文１）は前提から結論が正しく導けますが、（文２）では前提から結論を正しく導いているとは言えませんから。
　（文２）は論理的にぶっ飛んでいます。確かにそのとおりです。でも、（文１）を使って結論が正しいことを示そうとしたら、もっと激しくぶっ飛ぶしかないのです。

　そのことを図に表すと、右のようになります。図の階段の高さは「情報量」を表しています。

（文２）は上にジャンプしています。先ほどは「ぶっ飛ぶ」と言いましたが、「論理が飛躍している」と言ってもいいでしょう。
　一方、階段を降りるようなイメージのものが（文１）です。前提の方が情報量が多くて、論証を進めるうちにだんだんと情報量が減っていって、結論に至ります。ここには一切の飛躍はありません。「前提から結論を正しく導く」というのはそういうことです。
　けれども、そのことと「結論が正しい」かどうかは別物で、結論が正しいことを示すためには、前提が正しいことを示さなければならなくて、そのためには（文２）のジャンプよりはるかに大きなジャンプ（論理の飛躍）をしなければならないのです。そして、そうなると飛躍が大きい分、（文２）よりよっぽど怪しい議論になるでしょう。結局のところ（文１）で「結論が正しい」ことを示そうとすると、無駄に遠回りをして、無茶な飛躍をして、論理的に破綻するのがオチなのです。

　では、どうすればいいのでしょう？　単純な話です。（文２）で語ればいいのです。「○○が～～と言ったこと」が「○○はバカだ」と判断する十分な根拠になると思えば、「○○はバカだ」と判断すればいいのです（それを公言・放言するかどうかは、また別の話です）。
　（文２）で語るときのポイントは説得力です。根拠をきちんと説明することです。でも、絶対に「正しい論理」になんかなりません。それでいいんです。
　記事「論理には４種類ある」で論理を「記号論理」（命題論理）と「数学の論理」と「科学の論理」と「議論の論理」の４つに分けました。（文１）の論理が「記号論理」（命題論理）です。（文２）の論理が「議論の論理」です。

カラスは黒いのか？　　「ソクラテスは死ぬ」のか？　　バカを論証する

◎ モデル化の技術

　カリキュラム「モデル化とシミュレーション」の紹介です。いろんな自然現象・社会現象をモデル化して、エクセルでシミュレーションして、最後はグラフで視覚化します。
　授業時間は想定 8 時間。その流れをいくつかの記事に分けて書いています。

授業	記事	実習
序章	モデル化とシミュレーション	－
	自然現象・社会現象をモデルで斬る	－
1	コインを投げる	モデル化 → シミュレーション
	サイコロを投げる	それぞれ100回投げてみよう
2	埃が風に舞う	１つの埃が風に舞って移動する様子
	埃は部屋の隅にたまる	部屋の隅に埃がたまる様子
3	図解モデルの描き方	－
	数式モデルの書き方	－
4	図解モデルの基本形	積立貯金の残高
	車は無限に速くなる？	アクセルを踏み続けるときの車の速度
5	やかんのお湯が冷める	お湯が冷めるときの温度変化
	温度変化にはわけがある	エアコンのサーモスタット機能
6	食物連鎖を再現する	羊は草を食べて育つ
	めざせ、地球シミュレータ	CO2濃度と気温の関係
7	Ｓ字カーブを描いてみよう	頭打ちネズミ算
	人のうわさも75日	うわさ終息曲線
8	フェルミ推定とは？	日本中に電信柱は何本あるか？
	フェルミ推定してみよう	ラーメン屋の親父の年収は？　他
終章	「モデル化とシミュレーション」の効能	－

最後に・・・ネタ求む。